题目内容
28+210+2n是完全平方数,求n的值.
考点:完全平方数
专题:
分析:直接利用a2+b2+2ab=(a+b)2,分别使每一项与公式对应用分析求出n的值.
解答:解:∵a2+b2+2ab=(a+b)2,
∴若28=a2,210=b2,
则a=24,b=25,2n=2ab=210,解得:n=10
若28=a2,210=2ab,
所以b=25 ,
则2n=b2=210,
解得:n=10,
若210=a2,28=2ab,
所以b=22 ,
则2n=b2=24,
解得:n=4,
所以n=4或n=10.
∴若28=a2,210=b2,
则a=24,b=25,2n=2ab=210,解得:n=10
若28=a2,210=2ab,
所以b=25 ,
则2n=b2=210,
解得:n=10,
若210=a2,28=2ab,
所以b=22 ,
则2n=b2=24,
解得:n=4,
所以n=4或n=10.
点评:此题主要考查了完全平方数的定义,正确利用完全平方公式分析得出是解题关键.

练习册系列答案
相关题目
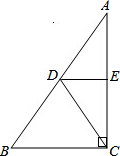 如图,在△ABC中,∠ACB=90°,点D是斜边AB的中点,AE=CE,求证:∠CDE=∠B.
如图,在△ABC中,∠ACB=90°,点D是斜边AB的中点,AE=CE,求证:∠CDE=∠B.