题目内容
如图,正方形ABCD的边长为2,点E在边AD上(不与A、D重合),点F在边CD上,且∠EBF=45°.△ABE的外接圆O与BC、BF分别交于点G、H.
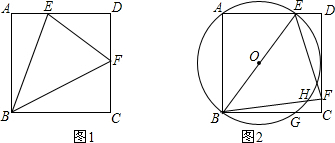
(1)在图1中作出圆O,并标出点G和点H;
(2)若EF∥AC,试说明
与
的大小关系,并说明理由;
(3)如图2所示,若圆O与CD相切,试求△BEF的面积.

(1)在图1中作出圆O,并标出点G和点H;
(2)若EF∥AC,试说明
 |
| BG |
 |
| GH |
(3)如图2所示,若圆O与CD相切,试求△BEF的面积.
考点:圆的综合题
专题:
分析:(1)根据题意利用同一圆中相等的弦所对的圆周角相等画出图形即可;
(2)连接BD、EG、EH,先由已知得出BD为EF的中垂线,再得出∠BEG=22.5°=∠HBG,即可得出
=
;
(3)将△BCF绕点B逆时针旋转90°到△BAP,过点B作BQ⊥EF,设⊙O与CD相切于点M,连接OM,延长MO交AB于点N,由已知得出△BPE≌△BFE,进而得出△AEB≌△QEB,可得C△EFD=4,再利用中位线出a的值,利用直角三角形得出b的值,即可求出△BEF的面积.
(2)连接BD、EG、EH,先由已知得出BD为EF的中垂线,再得出∠BEG=22.5°=∠HBG,即可得出
 |
| BG |
 |
| GH |
(3)将△BCF绕点B逆时针旋转90°到△BAP,过点B作BQ⊥EF,设⊙O与CD相切于点M,连接OM,延长MO交AB于点N,由已知得出△BPE≌△BFE,进而得出△AEB≌△QEB,可得C△EFD=4,再利用中位线出a的值,利用直角三角形得出b的值,即可求出△BEF的面积.
解答:解:(1)如图1,

(2)如图2,连接BD、EG、EH,

∵EF∥AC,
∴DE=DF,
又∵BD平分∠EDF,
∴BD为EF的中垂线,
∴BE=BF,BD平分∠EBF,
又∵∠EBF=45°=∠DBC,
∴∠EBD=∠DBF=∠HBG=22.5°,
∴∠EBG=67.5°,
又∵∠EGB=90°,
∴∠BEG=22.5°=∠HBG,
∴
=
,
(3)如图3,将△BCF绕点B逆时针旋转90°到△BAP,过点B作BQ⊥EF,设⊙O与CD相切于点M,连接OM,延长MO交AB于点N,

在△BPE与△BFE中,
,
∴△BPE≌△BFE(SAS),
∴∠AEB=∠BEQ,PE=EF,
由∠AEB=∠BEQ可知,
在△AEB和△QEB中,
,
∴△AEB≌△QEB(AAS),
∴BQ=AB=2,
由PE=EF可知,
C△EFD=ED+DF+EF=ED+DF+PE=ED+DF+PA+AE=ED+AE+DF+FC=4,
设AE=a,DF=b,则DE=2-a,BE=
,
∵O为BE中点,且MN∥AD,
∴ON=
=
,
∴OM=2-
,
又BE=2OM,
∴
=4-a,解得a=
,
∴ED=
,
又∵C△EFD=4,DF=b,
∴EF=4-b-
=
-b,
在RT△EDF中,(
)2+b2=(
-b)2,解得b=
,
∴EF=
-
=
,
∴S△BEF=
×
×2=
.

(2)如图2,连接BD、EG、EH,

∵EF∥AC,
∴DE=DF,
又∵BD平分∠EDF,
∴BD为EF的中垂线,
∴BE=BF,BD平分∠EBF,
又∵∠EBF=45°=∠DBC,
∴∠EBD=∠DBF=∠HBG=22.5°,
∴∠EBG=67.5°,
又∵∠EGB=90°,
∴∠BEG=22.5°=∠HBG,
∴
 |
| BG |
 |
| GH |
(3)如图3,将△BCF绕点B逆时针旋转90°到△BAP,过点B作BQ⊥EF,设⊙O与CD相切于点M,连接OM,延长MO交AB于点N,

在△BPE与△BFE中,
|
∴△BPE≌△BFE(SAS),
∴∠AEB=∠BEQ,PE=EF,
由∠AEB=∠BEQ可知,
在△AEB和△QEB中,
|
∴△AEB≌△QEB(AAS),
∴BQ=AB=2,
由PE=EF可知,
C△EFD=ED+DF+EF=ED+DF+PE=ED+DF+PA+AE=ED+AE+DF+FC=4,
设AE=a,DF=b,则DE=2-a,BE=
| 4+a2 |
∵O为BE中点,且MN∥AD,
∴ON=
| AE |
| 2 |
| a |
| 2 |
∴OM=2-
| a |
| 2 |
又BE=2OM,
∴
| 4+a2 |
| 3 |
| 2 |
∴ED=
| 1 |
| 2 |
又∵C△EFD=4,DF=b,
∴EF=4-b-
| 1 |
| 2 |
| 7 |
| 2 |
在RT△EDF中,(
| 1 |
| 2 |
| 7 |
| 2 |
| 12 |
| 7 |
∴EF=
| 7 |
| 2 |
| 12 |
| 7 |
| 25 |
| 14 |
∴S△BEF=
| 1 |
| 2 |
| 25 |
| 14 |
| 25 |
| 14 |
点评:本题主要考查了圆的综合题,解题的关键是正确作出辅助线,利用三解形全等及方程灵活的求解.

练习册系列答案
 考前必练系列答案
考前必练系列答案
相关题目
在同一平面直角坐标系中,将函数y=2x2+4x+1的图象沿x轴方向向右平移2个单位后再沿y轴向下平移1个单位,得到图象的顶点坐标是( )
| A、(-1,1) |
| B、(1,-2) |
| C、(2,-2) |
| D、(1,-2) |
一个扇形的圆心角为120°,半径为3,则这个扇形的面积为( )
| A、3π | B、9π | C、2π | D、4π |
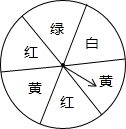 如图,有一个转盘被分成6个相同的扇形区域,颜色分别为红、黄、绿、白四中颜色,指针的位置固定,转动转盘后任其自由停止,如果指针指在等分线上,那么重新转动,直至指针指向某个扇形区域内为止,请你完成以下问题:
如图,有一个转盘被分成6个相同的扇形区域,颜色分别为红、黄、绿、白四中颜色,指针的位置固定,转动转盘后任其自由停止,如果指针指在等分线上,那么重新转动,直至指针指向某个扇形区域内为止,请你完成以下问题: 如图,水库大坝的横截面是梯形,坝顶AD宽5米,坝高10米,斜坡CD的坡角为45°,斜坡AB的坡度i=1:1.5,那么坝底BC的长度为
如图,水库大坝的横截面是梯形,坝顶AD宽5米,坝高10米,斜坡CD的坡角为45°,斜坡AB的坡度i=1:1.5,那么坝底BC的长度为