题目内容
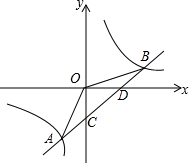 如图,一次函数y1=kx+b的图象与反比例函数y2=
如图,一次函数y1=kx+b的图象与反比例函数y2=| m |
| x |
(1)求反比例函数y2=
| m |
| x |
(2)连接OA,OB.求△AOB的面积.
(3)根据图象,直接写出关于x的不等式
| m |
| x |
考点:反比例函数与一次函数的交点问题
专题:
分析:(1)根据待定系数法,可得反比例函数解析式,根据图象上的点满足函数解析式,可得B点坐标,再根据待定系数法,可得一次函数的解析式;
(2)根据三角形面积的和差,可得答案;
(3)根据函数与不等式的关系,可得答案.
(2)根据三角形面积的和差,可得答案;
(3)根据函数与不等式的关系,可得答案.
解答:解:(1)由反比例函数y2=
的图象经过点A(-2,-5),得
m=xy=(-2)×(-5)=10,
故反比例函数解析式为y=
,
点B在反比例函数图象上,得
n=
=2,B点坐标是(5,2),
一次函数图象经过A、B点,得
,
解得
.
故一次函数的解析式为y=x-3;
(2)当y=0时,x-3=0,解得x=3,
S△AOB=S△BOD+S△AOD
=
×3×2+
×3×|-5|
=3+
=
;
(3)由反比例函数图象在一次函数图象下方,得-2<x<0或x>5.
| m |
| x |
m=xy=(-2)×(-5)=10,
故反比例函数解析式为y=
| 10 |
| x |
点B在反比例函数图象上,得
n=
| 10 |
| 5 |
一次函数图象经过A、B点,得
|
解得
|
故一次函数的解析式为y=x-3;
(2)当y=0时,x-3=0,解得x=3,
S△AOB=S△BOD+S△AOD
=
| 1 |
| 2 |
| 1 |
| 2 |
=3+
| 15 |
| 2 |
=
| 21 |
| 2 |
(3)由反比例函数图象在一次函数图象下方,得-2<x<0或x>5.
点评:本题考查了反比例函数与一次函数的交点问题,利用了待定系数法求函数解析式,利用函数图象解不等式.

练习册系列答案
相关题目
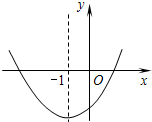 二次函数y=mx2+2mx-(3-m)的图象如图所示,则m的取值范围是( )
二次函数y=mx2+2mx-(3-m)的图象如图所示,则m的取值范围是( )| A、m<3 | B、m>3 |
| C、m>0 | D、0<m<3 |
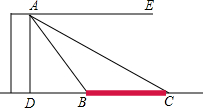 如图,塔AD的高度为30m,塔的底部D与桥BC位于同一条水平直线上.由塔顶A测得B和C的俯角∠EAB,∠EAC分别为60°和30°.求BD,BC的长.(结果精确到0.01m)
如图,塔AD的高度为30m,塔的底部D与桥BC位于同一条水平直线上.由塔顶A测得B和C的俯角∠EAB,∠EAC分别为60°和30°.求BD,BC的长.(结果精确到0.01m)



