题目内容
1.为寻求合适的销售价格,商场对新进的一种商品进行了一周的试销,发现这种商品的每天销售量y(千克)与销售价格x(元/千克)之间成反比例关系,已知第一天以220元/千克的价格销售了80千克.(1)求y与x的函数关系式;
(2)试销期间共销售了700千克这种新进的商品,在试销后,商场决定将这种新进商品的销售价格定为160元/千克,这样按所发现的反比例关系预测剩余这种商品再用10天可以全部售完.问商场共新进多少千克的这种商品?
分析 (1)根据第一天以220元/千克的价格销售了80千克利用待定系数法确定反比例函数的解析式即可;
(2)将x=160代入求得每天的销售量即可求得总销售量,从而求得购进的商品的数量.
解答 解:(1)设每天销售量y(千克)与销售价格x(元/千克)之间成反比例关系为y=$\frac{k}{x}$,
∵第一天以220元/千克的价格销售了80千克,
∴k=220×80=17600,
∴y与x的函数关系式为y=$\frac{17600}{x}$;
(2)当x=160时,y=110,
故总进货量为700+10×110=1800千克.
点评 本题考查了反比例函数的应用,解题的关键是从实际问题中抽象出反比例函数模型,难度不大.

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案
相关题目
9.关于x的一元二次方程ax2-x+1=0有实数根,则a的取值范围是( )
| A. | a≤$\frac{1}{4}$且a≠0 | B. | a≤$\frac{1}{4}$ | C. | a≥$\frac{1}{4}$且a≠0 | D. | a≥$\frac{1}{4}$ |
11.将抛物线y=2x2+1向左平移1个单位,再向下平移3个单位后所得到的抛物线为( )
| A. | y=2(x+1)2-2 | B. | y=2(x+1)2+4 | C. | y=2(x-1)2-2 | D. | y=2(x-1)2+4 |
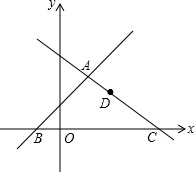 如图,在平面直角坐标系xOy中,直线l1:y=x+1与直线l2:y=kx+3交于点A,分别交x轴于点B和点C(4,0),点D是直线l2上的一个动点,
如图,在平面直角坐标系xOy中,直线l1:y=x+1与直线l2:y=kx+3交于点A,分别交x轴于点B和点C(4,0),点D是直线l2上的一个动点,