题目内容
6．化简：（$\frac{{m}^{2}-6m+9}{{m}^{2}-9}$-$\frac{m}{m+3}$）÷$\frac{m-1}{m+3}$．分析 原式括号中两项通分并利用同分母分式的减法法则计算，同时利用除法法则变形，约分即可得到结果．
解答 解：原式=[$\frac{（m-3）^{2}}{（m+3）（m-3）}$-$\frac{m（m-3）}{（m+3）（m-3）}$]•$\frac{m+3}{m-1}$
=$\frac{-3（m-3）}{（m+3）（m-3）}$•$\frac{m+3}{m-1}$
=$\frac{3}{1-m}$．
点评 此题考查了分式的混合运算，熟练掌握运算法则是解本题的关键．
练习册系列答案
相关题目
16．截止到2015年4月9日0时，北京小客车指标申请累计收到个人申请491671个，第四轮摇号中签率接近28比1．将491671用科学记数法表示应为（ ）
| A． | 49.1671×104 | B． | 4.91671×105 | C． | 4.91671×106 | D． | 0.491671×107 |
17．
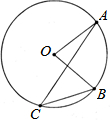如图，⊙O上A、B、C三点，若∠B=50°，∠A=20°，则∠AOB等于（ ）
如图，⊙O上A、B、C三点，若∠B=50°，∠A=20°，则∠AOB等于（ ）| A． | 30° | B． | 50° | C． | 70° | D． | 60° |
14．
如图，直径为10的⊙A经过点C（0，5）和点O （0，0），B是y轴右侧⊙A优弧上一点，则tan∠OBC的值为（ ）
如图，直径为10的⊙A经过点C（0，5）和点O （0，0），B是y轴右侧⊙A优弧上一点，则tan∠OBC的值为（ ）| A． | $\frac{1}{2}$ | B． | $\frac{\sqrt{3}}{2}$ | C． | $\frac{{\sqrt{3}}}{3}$ | D． | $\sqrt{3}$ |
1．关于x的一元二次方程（m-1）x2-2mx+m+1=0（ ）
| A． | 方程有两个不相等的实数根 | B． | 方程有两个相等的实数根 | ||
| C． | 方程无实数根 | D． | 方程的实数根与m有关 |
11．某中学为了解学生的视力情况，需要抽取部分学生进行调查，下列抽取方法中最合适的是（ ）
| A． | 随机抽取一部分男生 | |
| B． | 随机抽取一个班级的学生 | |
| C． | 随机抽取一个年级的学生 | |
| D． | 在各个年级中，每班各随机抽取20名学生 |
18．$\sqrt{3}$的相反数是（ ）
| A． | $\sqrt{3}$ | B． | $\frac{{\sqrt{3}}}{3}$ | C． | -$\sqrt{3}$ | D． | -$\frac{\sqrt{3}}{3}$ |
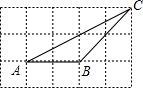如图，每个小正方形的边长为1，△ABC的顶点都在方格纸的格点上，则sinA=$\frac{\sqrt{5}}{5}$．