题目内容
如图，已知∠B=90°，AB=3cm，BC=
cm，点D是线段BC上的一个动点，连接AD，动点B′始终保持与点B关于直线AD对称，当点D由点B位置向右运动至点C位置时，相应的点B′所经过的路程为________cm．
π
分析：首先利用三角函数即可求得∠BAC=30度，则当点D由点B位置向右运动至点C位置时，相应的点B′所经过的路径是以A为圆心，以AB为半径，圆心角是60度的弧，利用弧长公式即可求解．
解答：
解：连接AC，
∵直角△ABC中，AB=3cm，BC=cm，
∴tan∠BAC=
=
，
∴∠BAC=30°，
当点D由点B位置向右运动至点C位置时，相应的点B′所经过的路径是以A为圆心，以AB为半径，圆心角是60度的弧，
则相应的点B′所经过的路程是
=π．
故答案是：π．
点评：本题考查了弧长的计算公式，正确理解点B′所经过的路径是以A为圆心，以AB为半径，圆心角是60度的弧是关键．
分析：首先利用三角函数即可求得∠BAC=30度，则当点D由点B位置向右运动至点C位置时，相应的点B′所经过的路径是以A为圆心，以AB为半径，圆心角是60度的弧，利用弧长公式即可求解．
解答：
解：连接AC，∵直角△ABC中，AB=3cm，BC=
cm，∴tan∠BAC=
=，∴∠BAC=30°，
当点D由点B位置向右运动至点C位置时，相应的点B′所经过的路径是以A为圆心，以AB为半径，圆心角是60度的弧，
则相应的点B′所经过的路程是
=π．故答案是：π．
点评：本题考查了弧长的计算公式，正确理解点B′所经过的路径是以A为圆心，以AB为半径，圆心角是60度的弧是关键．
练习册系列答案
口算题天天练系列答案
相关题目
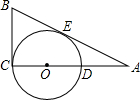如图，已知∠C=90°，点O在AC上，CD为⊙O的直径，⊙O切AB于点E，若BC=5，AC=12，求⊙O的半径．
如图，已知∠ABC=90°，射线BD上有一点P（点P与点B不重合），且点P到BA，BC的距离分别为PE、PF，PH⊥BD交BC于H，设∠ABD=α，PB=m．
如图，已知∠AOC=90°，∠COD比∠DOA大28°，OB是∠AOC的平分线．求∠BOD的度数．
如图，已知∠C=90°，BC=3cm，BD=12cm，AD=13cm．△ABC的面积是6cm2．
（2012•厦门）如图，已知∠ABC=90°，AB=πr，BC=