题目内容
 如图,已知∠C=90°,BC=3cm,BD=12cm,AD=13cm.△ABC的面积是6cm2.
如图,已知∠C=90°,BC=3cm,BD=12cm,AD=13cm.△ABC的面积是6cm2.(1)求AB的长度;
(2)求△ABD的面积.
分析:(1)根据直角三角形ABC的面积求得AC,再根据勾股定理即可求得AB的长;
(2)根据勾股定理的逆定理证明△ABD是直角三角形,即可求解.
(2)根据勾股定理的逆定理证明△ABD是直角三角形,即可求解.
解答:解:(1)∵∠C=90°
∴S三角形ABC=
×BC×AC=6,
∴AC=4(cm).
∵BC2+AC2=AB2,
∴AB=
=
=5(cm).
(2)∵AB2+BD2=52+122=169,AD2=132=169,
∴AB2+BD2=AD2.
∴∠ABD=90°.
∴S△ABD=
×AB×BD=
×5×12=30(cm2).
∴S三角形ABC=
| 1 |
| 2 |
∴AC=4(cm).
∵BC2+AC2=AB2,
∴AB=
| BC2+AC2 |
| 32+42 |
(2)∵AB2+BD2=52+122=169,AD2=132=169,
∴AB2+BD2=AD2.
∴∠ABD=90°.
∴S△ABD=
| 1 |
| 2 |
| 1 |
| 2 |
点评:此题主要是考查了勾股定理及其逆定理.
注意:直角三角形的面积等于两条直角边的乘积的一半.
注意:直角三角形的面积等于两条直角边的乘积的一半.

练习册系列答案
相关题目
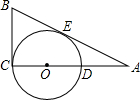 如图,已知∠C=90°,点O在AC上,CD为⊙O的直径,⊙O切AB于点E,若BC=5,AC=12,求⊙O的半径.
如图,已知∠C=90°,点O在AC上,CD为⊙O的直径,⊙O切AB于点E,若BC=5,AC=12,求⊙O的半径. 如图,已知∠ABC=90°,射线BD上有一点P(点P与点B不重合),且点P到BA,BC的距离分别为PE、PF,PH⊥BD交BC于H,设∠ABD=α,PB=m.
如图,已知∠ABC=90°,射线BD上有一点P(点P与点B不重合),且点P到BA,BC的距离分别为PE、PF,PH⊥BD交BC于H,设∠ABD=α,PB=m. 如图,已知∠AOC=90°,∠COD比∠DOA大28°,OB是∠AOC的平分线.求∠BOD的度数.
如图,已知∠AOC=90°,∠COD比∠DOA大28°,OB是∠AOC的平分线.求∠BOD的度数. (2012•厦门)如图,已知∠ABC=90°,AB=πr,BC=
(2012•厦门)如图,已知∠ABC=90°,AB=πr,BC=