题目内容
4.不等式组$\left\{\begin{array}{l}{x-a≥0}\\{x-a≤1}\end{array}\right.$的解集中任何x的值均在2≤x≤5的范围内,则a的取值范围是( )| A. | a≥2 | B. | 2≤a≤4 | C. | a≤4 | D. | a≥2且a≠4 |
分析 首先求出不等式组$\left\{\begin{array}{l}{x-a≥0}\\{x-a≤1}\end{array}\right.$的解集是多少,然后根据不等式组$\left\{\begin{array}{l}{x-a≥0}\\{x-a≤1}\end{array}\right.$的解集中任何x的值均在2≤x≤5的范围内,求出a的取值范围即可.
解答 解:∵$\left\{\begin{array}{l}{x-a≥0}\\{x-a≤1}\end{array}\right.$,
∴a≤x≤a+1,
∵不等式组$\left\{\begin{array}{l}{x-a≥0}\\{x-a≤1}\end{array}\right.$的解集中任何x的值均在2≤x≤5的范围内,
∴$\left\{\begin{array}{l}{a≥2}\\{a+1≤5}\end{array}\right.$
∴a的取值范围是:2≤a≤4.
故选:B.
点评 此题主要考查了不等式组的解集,要熟练掌握,解答此题的关键是求出不等式组$\left\{\begin{array}{l}{x-a≥0}\\{x-a≤1}\end{array}\right.$的解集是多少.

练习册系列答案
相关题目
 如图,AB与CD相交于点O,若∠DOE=90°,∠BOE=53°,则∠AOC=37°.
如图,AB与CD相交于点O,若∠DOE=90°,∠BOE=53°,则∠AOC=37°. 如图,在直角坐标系中,四边形ABCD各个顶点的坐标分别是A(0,0)、B(3,6)、C(10,8)、D(13,0),确定这个四边形的面积.
如图,在直角坐标系中,四边形ABCD各个顶点的坐标分别是A(0,0)、B(3,6)、C(10,8)、D(13,0),确定这个四边形的面积.
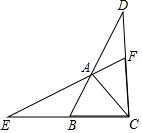 如图,△ABC是等边三角形,延长BA到点D,延长CB到点E,使BE=AD,连接CD,AE.
如图,△ABC是等边三角形,延长BA到点D,延长CB到点E,使BE=AD,连接CD,AE.