题目内容
19.已知等腰△OAB和等腰△OCD,OA=OB,OC=OD,∠AOB=∠COD,O,C,B在一条直线上,连AC,过B作BE∥AC交直线OA于点E.①如图(1),当∠AOB=∠COD=60°时,∠EBD=120°;
②如图(2),当∠AOB=∠COD=90°时,∠EBD=90°.

分析 根据已知条件证得△AOC≌△BOD,由全等三角形的性质得到∠ACO=∠BDO,根据平行线的性质得到∠ACO=∠EBO,等量代换得到∠EBO=∠BDO,于是得到∠EBD=∠OBE+∠OBD=∠ODB+∠OBD=180°-∠DOB,①由∠DOB=60°,即可得到∠EBD=120°,②由∠DOB=90°,即可得到∠EBD=90°.
解答 解:在△AOC与△BOD中,$\left\{\begin{array}{l}{AO=BO}\\{∠AOC=∠BOD}\\{OC=OD}\end{array}\right.$,
∴△AOC≌△BOD,
∴∠ACO=∠BDO,
∵AC∥BE,
∴∠ACO=∠EBO,
∴∠EBO=∠BDO,
∴∠EBD=∠OBE+∠OBD=∠ODB+∠OBD=180°-∠DOB,
①∵∠DOB=60°,
∴∠EBD=120°,
②∵∠DOB=90°,
∴∠EBD=90°.
故答案为:120°,90°.
点评 本题考查了全等三角形的判定和性质,三角形的内角和,平行线的性质,熟练掌握全等三角形的判定和性质是解题的关键.

练习册系列答案
相关题目
16.若等腰直角三角形的外接圆半径的长为$\sqrt{2}$,则其内切圆半径的长为( )
| A. | $2\sqrt{2}-1$ | B. | $2\sqrt{2}-2$ | C. | $2-\sqrt{2}$ | D. | $\sqrt{2}-1$ |
 如图,平行四边形ABCD中,对角线AC、BD相交于点O,BD=2AD,E、F、G分别是OC、
如图,平行四边形ABCD中,对角线AC、BD相交于点O,BD=2AD,E、F、G分别是OC、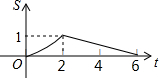



 如图,△ABC中,∠BAC=90°,取BF=AB,作DF⊥BC交AC于D,作AE⊥BC于E.
如图,△ABC中,∠BAC=90°,取BF=AB,作DF⊥BC交AC于D,作AE⊥BC于E.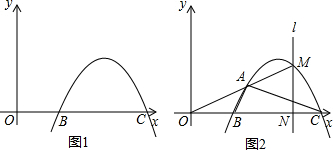
 已知:如图,在四边形ABCD中,∠A=∠B=90°,AB=AD=18,∠CDE=45°,CE=15,求线段AE的长.
已知:如图,在四边形ABCD中,∠A=∠B=90°,AB=AD=18,∠CDE=45°,CE=15,求线段AE的长. 已知,如图,在△ABC中,已知AB=AC=5cm,BC=6cm.点P从点B出发,沿BA方向匀速运动,速度为1cm/s;同时,直线QD从点C出发,沿CB方向匀速运动,速度为1cm/s,且QD⊥BC,与AC,BC分别交于点D,Q;当直线QD停止运动时,点P也停止运动.连接PQ,设运动时间为t(0<t<3)s.解答下列问题:
已知,如图,在△ABC中,已知AB=AC=5cm,BC=6cm.点P从点B出发,沿BA方向匀速运动,速度为1cm/s;同时,直线QD从点C出发,沿CB方向匀速运动,速度为1cm/s,且QD⊥BC,与AC,BC分别交于点D,Q;当直线QD停止运动时,点P也停止运动.连接PQ,设运动时间为t(0<t<3)s.解答下列问题: