题目内容
2.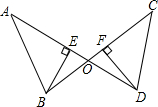 如图,AD和BC相交于点O,BE⊥AD于点E,DF⊥BC于点F,BE=DF,∠ABC=∠CDA.求证:AB=CD.
如图,AD和BC相交于点O,BE⊥AD于点E,DF⊥BC于点F,BE=DF,∠ABC=∠CDA.求证:AB=CD.
分析 首先证明△OBE≌△ODF得到OB-OD,然后证明△ABO≌△CDO,根据全等三角新的对应边相等即可证得.
解答 证明:∵△OBE和△ODF中,$\left\{\begin{array}{l}{∠BOE=∠DOF}\\{∠BEO=∠DFO}\\{BE=DF}\end{array}\right.$,
∴△OBE≌△ODF,
∴OB=OD,
∴在△ABO和△CDO中,$\left\{\begin{array}{l}{∠AOB=∠COD}\\{OB=OD}\\{∠ABC=∠CDA}\end{array}\right.$,
∴△ABO≌△CDO,
∴AB=CD.
点评 本题考查了全等三角形的判定与性质,证明线段相等的常用方法是转化为证明三角形全等.

练习册系列答案
相关题目
3.如果3x2n-1ym与-5xmy-3是同类项,则mn( )
| A. | -3 | B. | -4 | C. | 3 | D. | 4 |
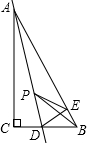 如图,在Rt△ABC中,∠C=90°,AC=4,CB=3,点D是BC边上的点,将△ADC沿直线AD翻折,使点C落在AB边上的点E处,若点P是直线AD上的动点,则△PEB的周长的最小值是4.
如图,在Rt△ABC中,∠C=90°,AC=4,CB=3,点D是BC边上的点,将△ADC沿直线AD翻折,使点C落在AB边上的点E处,若点P是直线AD上的动点,则△PEB的周长的最小值是4.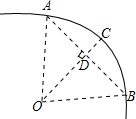 如图,一条公路的转弯处是一段圆弧(图中的弧AB),点O是这段弧的圆心,C是弧AB上一点,OC⊥AB,垂足为D.若这段弯路的半径是100m,CD=20m,则A、B两点的直线距离是( )
如图,一条公路的转弯处是一段圆弧(图中的弧AB),点O是这段弧的圆心,C是弧AB上一点,OC⊥AB,垂足为D.若这段弯路的半径是100m,CD=20m,则A、B两点的直线距离是( )