题目内容
18.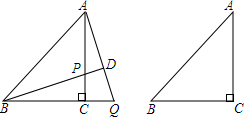 在△ABC中,BC=AC,∠BCA=90°,P为直线AC上一点,过A作AQ⊥BP于D,交直线BC于Q.
在△ABC中,BC=AC,∠BCA=90°,P为直线AC上一点,过A作AQ⊥BP于D,交直线BC于Q.(1)如图1,当P在线段AC上时,求证:BP=AQ.
(2)如图2,当P在线段CA的延长线上时,其它条件不变,连PQ,请画出图形,猜想AB与PQ之间的位置关系并证明.
(3)在(2)的条件下,当∠DBQ的度数为67.5°时,存在AQ=2BD.
分析 (1)首先根据内角和定理得出∠DAP=∠CBP,进而得出△ACQ≌△BCP即可得出答案;
(2)延长BA交PQ于H,由于∠ACQ=∠BDQ=90°,∠AQC=∠BQD,得到∠CAQ=∠DBQ,推出△AQC≌△BPC(ASA),根据全等三角形的性质得到QC=CP,由于∠QCD=90°,于是得到∠CQP=∠CPQ=45°,根据∠ABC=∠PQC=45°,于是得到∠BHQ=90°,即可得到结论;
(3)当∠DBQ=67.5°时,存在AQ=2BD,由∠DBQ=67.5°,∠ABC=45°,得到∠PBA=∠DBQ-∠ABC=22.5°,根据∠BAC=∠DBA+∠APB,∠BAC=45°,推出∠PBA=∠APB=22.5°根据等腰三角形的性质得到BP=2BD,通过△PBC≌△ACQ,根据全等三角形的性质即可得到结论.
解答 (1)证明:∵∠ACB=∠ADB=90°,∠APD=∠BPC,
∴∠DAP=∠CBP,
在△ACQ和△BCP中
$\left\{\begin{array}{l}{∠QCA=∠PCB}\\{CA=CB}\\{∠CAQ=∠CBP}\end{array}\right.$,
∴△ACQ≌△BCP(ASA),
∴BP=AQ;
(2)延长BA交PQ于H,∵∠ACQ=∠BDQ=90°,∠AQC=∠BQD,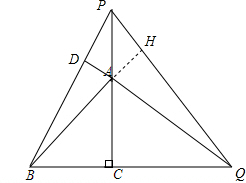
∴∠CAQ=∠DBQ,
在△AQC和△BPC中
$\left\{\begin{array}{l}{∠ACQ=∠BCP}\\{CA=CB}\\{∠CAQ=∠CBP}\end{array}\right.$,
∴△AQC≌△BPC(ASA),
∴QC=CP,
∵∠QCD=90°,
∴∠CQP=∠CPQ=45°,
∵∠ABC=∠PQC=45°,
∴∠BHQ=90°,
∴AB⊥PQ;
(3)当∠DBQ=67.5°时,存在AQ=2BD,
理由:∵∠DBQ=67.5°,∠ABC=45°,
∴∠PBA=∠DBQ-∠ABC=22.5°,
∵∠BAC=∠DBA+∠APB,
∵∠BAC=45°,
∴∠PBA=∠APB=22.5°,
∴AP=AB,
∵AD⊥BP,
∴BP=2BD,
在△PBC与△QAC中,
$\left\{\begin{array}{l}{∠BPC=∠AQC}\\{BC=AC}\\{∠PCB=∠ACQ}\end{array}\right.$,
∴△PBC≌△ACQ,
∴AQ=PB,
∴AQ=2BD.
故答案为:67.5°.
点评 此题主要考查了全等三角形的判定与性质以及等腰三角形性质和三角形内角和定理等知识,根据题意得出全等三角形是解题关键.

 同步练习强化拓展系列答案
同步练习强化拓展系列答案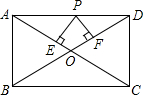 如图,在矩形ABCD中,AB=3,AD=4,P是AD上不与A、D重合的一动点,PE⊥AC,PF⊥BD,E、F为垂足,则PE+PF的值为( )
如图,在矩形ABCD中,AB=3,AD=4,P是AD上不与A、D重合的一动点,PE⊥AC,PF⊥BD,E、F为垂足,则PE+PF的值为( )| A. | 2 | B. | 2.4 | C. | 2.5 | D. | 2.6 |
| A. | 45° | B. | 36° | C. | 90° | D. | 135° |
 如图,在平面直角坐标系中,已知点P在坐标轴上,点B在第一象限,若三角形PBO是等腰三角形,则满足条件的P点的个数是7个.
如图,在平面直角坐标系中,已知点P在坐标轴上,点B在第一象限,若三角形PBO是等腰三角形,则满足条件的P点的个数是7个.