题目内容
8. 在△ABC中,AB=AC=4,∠A=α,P,Q分别是射线BA和AC延长线上的两点,且BP=CQ,连接PQ,与直线BC相交于点D,
在△ABC中,AB=AC=4,∠A=α,P,Q分别是射线BA和AC延长线上的两点,且BP=CQ,连接PQ,与直线BC相交于点D,(1)如图,当α=60°时,如果点P在线段AB上,那么AP的长度为多少时,∠APQ是一个直角;
(2)当α是一个定值时,过点P作PE⊥BC,交射线BC于点E,在点P、点Q的运动过程中,判断并说明DE的长度是否一个定值.
分析 (1)根据已知条件得到∠Q=30°,由直角三角形的性质得到AP=$\frac{1}{2}$AQ,设BP=x,则AP=4-x,AQ=4+x,列方程得到x=$\frac{8}{3}$,于是得到结论;
(2)作PF∥AQ,由平行线的性质得到∠PFB=∠ACB,根据等腰三角形的性质得到∠B=∠ACB,等量代换得到∠B=∠PFB,根据等腰三角形的判定得到BE=EF,PF=BP推出△PFD≌△QCD,根据全等三角形的性质得到DF=CD,推出DE=EF+FD=$\frac{1}{2}$BC,即可得到结论.
解答 解:(1)∵α=60°,PQ⊥AB,
∴∠Q=30°,
∴AP=$\frac{1}{2}$AQ,
∵AB=AC=4,
设BP=x,则AP=4-x,AQ=4+x,4-x=$\frac{1}{2}$(4+x),
∴x=$\frac{8}{3}$,
∴AP=$\frac{8}{3}$时,∠APQ=90°;
(2)作PF∥AQ,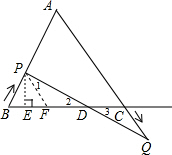 ∴∠PFB=∠ACB,
∴∠PFB=∠ACB,
∵△ABC为等腰三角形,
∴∠B=∠ACB,
∴∠B=∠PFB,
∴BE=EF,PF=BP,
∵PB=CQ,
∴CQ=PF,
∵PF∥AQ,
∴∠1=∠Q,
在△PFD与△QCD中,
$\left\{\begin{array}{l}{∠1=∠Q}\\{∠2=∠3}\\{PF=CQ}\end{array}\right.$,
∴△PFD≌△QCD,
∴DF=CD,
∴DE=EF+FD=$\frac{1}{2}$BC,
∴DF为定值.
点评 本题考查了全等三角形的判定和性质,等腰三角形的性质,平行线的性质,正确的作出辅助线是解题的关键.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案
相关题目
20.若a为实数,则下列说法正确的是( )
| A. | |-a|是正数 | B. | -|a|是负数 | C. | $\sqrt{{a}^{2}}$是非负数 | D. | |-a|永远大于-|a| |
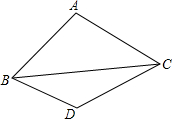 如图,在△ABC中,AB=AC,点D为△ABC外一点,且AC=CD,∠CBD=30°,求证:∠BDC=180°-$\frac{1}{2}$∠BAC.
如图,在△ABC中,AB=AC,点D为△ABC外一点,且AC=CD,∠CBD=30°,求证:∠BDC=180°-$\frac{1}{2}$∠BAC.