题目内容
8. 如图,破残的圆形轮片上,弦AB的垂直平分线交弧AB于C,交弦AB于D.求作此残片所在的圆(不写作法,保留作图痕迹).
如图,破残的圆形轮片上,弦AB的垂直平分线交弧AB于C,交弦AB于D.求作此残片所在的圆(不写作法,保留作图痕迹).
分析 由垂径定理知,垂直于弦的直径是弦的中垂线,故作AC,BC的中垂线交于点O,则点O是弧ACB所在圆的圆心.
解答  解:作弦AC的垂直平分线与弦AB的垂直平分线交于O点,以O为圆心OA长为半径作圆O就是此残片所在的圆,如图.
解:作弦AC的垂直平分线与弦AB的垂直平分线交于O点,以O为圆心OA长为半径作圆O就是此残片所在的圆,如图.
点评 本题考查的是垂径定理的应用,熟知“平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧”是解答此题的关键.

练习册系列答案
相关题目
19.一元二次方程x(x-1)=x的根为( )
| A. | x=2 | B. | x=0 | C. | x1=0,x2=2 | D. | x1=0,x2=1 |
16.下列函数中,y既不是x的正比例函数,也不是反比例函数的是( )
| A. | y=$\frac{1}{9x}$ | B. | $\frac{y}{2x}=1$ | C. | y=-3x2 | D. | $\frac{1}{5}$xy=-2 |
3.若⊙A和⊙B外切,它们的半径分别为8cm和2cm,则圆心距AB为( )
| A. | 6cm | B. | 6cm或10cm | C. | 10cm | D. | 4cm或6cm |
17.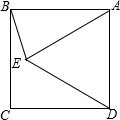 如图,在正方形ABCD的内部作等边△ADE,则∠AEB度数为( )
如图,在正方形ABCD的内部作等边△ADE,则∠AEB度数为( )
 如图,在正方形ABCD的内部作等边△ADE,则∠AEB度数为( )
如图,在正方形ABCD的内部作等边△ADE,则∠AEB度数为( )| A. | 80° | B. | 75° | C. | 70° | D. | 60° |
 将一张长方形纸片按如图所示折叠,如果∠1=58°,那么∠2=64°.
将一张长方形纸片按如图所示折叠,如果∠1=58°,那么∠2=64°.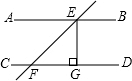 如图,已知直线AB∥CD,直线EF截AB、CD于E、F,EG⊥CD,∠EFD=45°且FG=6,则AB、CD之间的距离为6.
如图,已知直线AB∥CD,直线EF截AB、CD于E、F,EG⊥CD,∠EFD=45°且FG=6,则AB、CD之间的距离为6.