题目内容
18.函数y=$\frac{-{k}^{2}-2}{x}$(k为常数)的图象上有三点A(-3,y1),B(1,y2),C(2,y3),则函数值y1、y2、y3的大小关系是y2<y3<y1.分析 先判断出-k2-2的符号,再根据各点横坐标的值判断出A、B、C三点所在的象限,进而可得出结论.
解答 解:∵-k2-2<0,
∴函数y=$\frac{-{k}^{2}-2}{x}$(k为常数)的图象的两个分支分别位于二四象限,且在每一象限内,y随x的增大而增大.
∵-3<0,2>1>0,
∴点A(-3,y1)在第二象限,B(1,y2),C(2,y3)在第一象限,
∴y1>0,0>y3>y2,
∴y2<y3<y1.
故答案为:y2<y3<y1.
点评 本题考查的是反比例函数图象上点的坐标特点,熟知反比例函数的增减性是解答此题的关键.

练习册系列答案
相关题目
8.小明家冰箱冷冻室温度为-6℃,此时房屋内的温度为10℃,则房屋内的温度比冰箱冷冻室的温度高( )
| A. | 16℃ | B. | 4℃ | C. | -16℃ | D. | -4℃ |
6.若a=2+$\sqrt{5}$,b=$\frac{1}{2-\sqrt{5}}$,那么a与b的关系是( )
| A. | a<b且互为相反数 | B. | a>b且a与b互为相反数 | ||
| C. | a>b | D. | a=b |
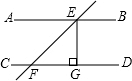 如图,已知直线AB∥CD,直线EF截AB、CD于E、F,EG⊥CD,∠EFD=45°且FG=6,则AB、CD之间的距离为6.
如图,已知直线AB∥CD,直线EF截AB、CD于E、F,EG⊥CD,∠EFD=45°且FG=6,则AB、CD之间的距离为6.
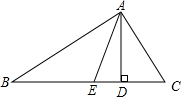 如图,在△ABC中,∠B=40°,∠C=60°,AD⊥BC于D,AE是∠BAC的平分线.
如图,在△ABC中,∠B=40°,∠C=60°,AD⊥BC于D,AE是∠BAC的平分线.