题目内容
3.甲船从A港出发顺流匀速驶向B港,乙船从B港出发逆流匀速驶向A港,甲船后面拖拽着一艘无动力小艇,行驶一段时间后,甲船发现拖拽小艇缆绳松了,小艇不知去向,立刻原路返回寻找,找到小艇后,继续拖拽小艇顺流驶向B港.已知小艇漂流的速度和水流速度相同;甲、乙两船在静水中的速度相同.甲、乙两船与A港的距离 y1、y2(km )与行驶时间x (h)之间的函数图象如图1所示.
(1)求乙船在逆流中行驶的速度;
(2)求甲船在逆流中行驶的路程;
(3)求甲船到A港的距离y1与行驶时间x之间的函数关系式;
(4)甲船拖拽的小艇与A港的距离y(km)和经历的时间x(h)之间的函数图象如图2所示,求点C的坐标.
分析 (1)由速度=路程÷时间列式求解;
(2)因为甲船、乙船在逆流中行驶的速度相同,只需由图示得出甲船在逆流中行驶的时间.
(3)观察图形,要分成3段讨论,每一段中已知两点,可用待定系数法确定一次函数的解析式.
(4)根据等量关系:救生圈落入水中后,船顺流行驶的路程=船逆流行驶的路程+救生圈漂流的路程,据此即可解答.
解答 解:(1)乙船在逆流中行驶的速度为6km/h.
(2)甲船在逆流中行驶的路程为6×(2.5-2)=3(km).
(3)设甲船顺流的速度为akm/h,
由图象得2a-3+(3.5-2.5)a=24,
解得a=9.(5分)
当0≤x≤2时,y1=9x,
当2≤x≤2.5时,设y1=-6x+b1,
把x=2,y1=18代入,得b1=30,
∴y1=-6x+30,
当2.5≤x≤3.5时,设y1=9x+b2,
把x=3.5,y1=24代入,得b2=-7.5,
∴y1=9x-7.5.
综上所述,y1=$\left\{\begin{array}{l}{9x}&{(0≤x≤2)}\\{-6x+30}&{(2<x≤\frac{5}{2})}\\{9x-\frac{15}{2}}&{(\frac{5}{2}<x≤\frac{7}{2})}\end{array}\right.$
(4)水流速度为(9-6)÷2=1.5(km/h),
设甲船从A港航行x小时救生圈掉落水中.
根据题意,得9(2-x)=1.5(2.5-x)+3,
解得x=1.5,
1.5×9=13.5,
即救生圈落水时甲船到A港的距离为13.5km.
∴点C坐标($\frac{3}{2}$,$\frac{27}{2}$).
点评 此题为一次函数的应用,渗透了函数与方程的思想,要求学生要提高阅读理解水平,从中挖掘有用信息,记住船顺流航行的速度=船在静水中航行的速度+水流速度,船逆流航行的速度=船在静水中航行的速度-水流速度.

 培优口算题卡系列答案
培优口算题卡系列答案 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案| A. |  | B. |  | C. |  | D. |  |
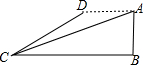 如图,飞机的高度AB=1000千米,从飞机上测得地面着陆点C的俯角为18°,飞机水平飞行一段距离后,到达D点,此时测得地面着陆点C的俯角为30°,求飞机飞行的距离AD的长(参考数据:$\sqrt{3}$≈1.73,$\sqrt{2}$≈1.41,tan18°≈0.32)
如图,飞机的高度AB=1000千米,从飞机上测得地面着陆点C的俯角为18°,飞机水平飞行一段距离后,到达D点,此时测得地面着陆点C的俯角为30°,求飞机飞行的距离AD的长(参考数据:$\sqrt{3}$≈1.73,$\sqrt{2}$≈1.41,tan18°≈0.32)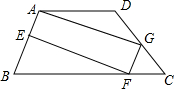 已知:如图所示,在四边形ABCD中,∠B=∠C,点E,F,G分别在AB,BC,CD上,且AE=GF=GC.
已知:如图所示,在四边形ABCD中,∠B=∠C,点E,F,G分别在AB,BC,CD上,且AE=GF=GC.