题目内容
9.关于x、y方程组$\left\{\begin{array}{l}x+y=3\\ x-2y=3a-3\end{array}\right.$的解满足x>y,求a的取值范围a>$\frac{1}{2}$.分析 把a看做已知数表示出方程组的解,代入已知不等式求出a的范围即可.
解答 解:$\left\{\begin{array}{l}{x+y=3①}\\{x-2y=3a-3②}\end{array}\right.$,
①-②得:3y=6-3a,即y=2-a,
把y=2-a代入①得:x=a+1,
代入不等式得:a+1>2-a,
解得:a>$\frac{1}{2}$,
故答案为:a>$\frac{1}{2}$
点评 此题考查了解一元一次不等式,以及二元一次方程组的解,熟练掌握运算法则是解本题的关键.

练习册系列答案
相关题目
19.人数相等的甲、乙两班学生参加同一次数学测验,班级平均分和方差分别为$\overline{{x}_{甲}}$=83分,$\overline{{x}_{乙}}$=83分,S甲2=245分,S乙2=190分,成绩较为整齐的是( )
| A. | 甲班 | B. | 乙班 | C. | 两班一样整齐 | D. | 无法确定 |
20.在$\frac{2}{7}$,$\root{3}{9}$,3.14,0.1010010001…,-$\sqrt{4}$,$\frac{π}{2}$这些数中,无理数有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
17.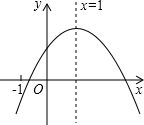 二次函数y=ax2+bx+c(a≠0)的图象如图所示,对称轴是直线x=1,则下列四个结论错误的是( )
二次函数y=ax2+bx+c(a≠0)的图象如图所示,对称轴是直线x=1,则下列四个结论错误的是( )
 二次函数y=ax2+bx+c(a≠0)的图象如图所示,对称轴是直线x=1,则下列四个结论错误的是( )
二次函数y=ax2+bx+c(a≠0)的图象如图所示,对称轴是直线x=1,则下列四个结论错误的是( )| A. | b>0 | B. | 2a+b=0 | C. | b2-4ac>0 | D. | a-b+c>0 |
4.满足$-\sqrt{7}$<x<$\sqrt{5}$的整数x有( )
| A. | 6个 | B. | 5个 | C. | 4个 | D. | 3个 |
14.若xy|m|-$\frac{1}{2}$(m+1)y-1是关于x、y的二次三项式,则m等于( )
| A. | -1 | B. | 1 | C. | ±1 | D. | 以上都不对 |
18.一次函数y=-2x+3的大致图象是( )
| A. |  | B. |  | C. |  | D. |  |
19.如果一个多边形的内角和是它的外角和的n倍,则这个多边形的边数是( )
| A. | n | B. | 2n-2 | C. | 2n | D. | 2n+2 |