题目内容
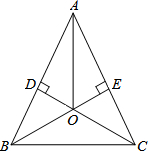 如图,AB=AC,CD⊥AB,BE⊥AC,垂足分别为点D,E,BE与CD相交于点O,连接BC,AO.求证:
如图,AB=AC,CD⊥AB,BE⊥AC,垂足分别为点D,E,BE与CD相交于点O,连接BC,AO.求证:(1)AD=AE;
(2)OA⊥BC.
考点:全等三角形的判定与性质,等腰三角形的性质
专题:证明题
分析:(1)根据垂直定义求出∠ADC=∠AEB=90°,根据AAS推出△ABE≌△ACD,根据全等三角形的判定推出即可;
(2)求出∠ADC=∠AEB=90°,根据HL推出Rt△ADO≌Rt△AEO,根据全等三角形的性质推出∠DAO=∠EAO,根据等腰三角形的性质推出即可.
(2)求出∠ADC=∠AEB=90°,根据HL推出Rt△ADO≌Rt△AEO,根据全等三角形的性质推出∠DAO=∠EAO,根据等腰三角形的性质推出即可.
解答:
证明:(1)∵CD⊥AB,BE⊥AC,
∴∠ADC=∠AEB=90°,
在△ABE和△ACD中
∴△ABE≌△ACD(AAS),
∴AD=AE;
(2)∵∠ADC=∠AEB=90°,
∴在Rt△ADO和Rt△AEO中
∴Rt△ADO≌Rt△AEO(HL),
∴∠DAO=∠EAO,
∵AB=AC,
∴AO⊥BC.
∴∠ADC=∠AEB=90°,
在△ABE和△ACD中
|
∴△ABE≌△ACD(AAS),
∴AD=AE;
(2)∵∠ADC=∠AEB=90°,
∴在Rt△ADO和Rt△AEO中
|
∴Rt△ADO≌Rt△AEO(HL),
∴∠DAO=∠EAO,
∵AB=AC,
∴AO⊥BC.
点评:本题考查了全等三角形的性质和判定,等腰三角形的性质的应用,解此题的关键是求出△ABE≌△ACD和Rt△ADO≌Rt△AEO,难度适中.

练习册系列答案
 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案 优翼小帮手同步口算系列答案
优翼小帮手同步口算系列答案
相关题目
 已知抛物线y=-x2+4x-3经过A(1,0),B(0,-3)两点,点P是抛物线的对称轴上的一点,连接PA,将线段PA绕着点A旋转90°得到线段P′A,若点P′恰好落在抛物线上,求点P的坐标.
已知抛物线y=-x2+4x-3经过A(1,0),B(0,-3)两点,点P是抛物线的对称轴上的一点,连接PA,将线段PA绕着点A旋转90°得到线段P′A,若点P′恰好落在抛物线上,求点P的坐标. 如图,△ABC中,AB=3,AC=4,BC=5.△ABD,△ACE,△BCF都是等边三角形,则四边形AEFD的面积为
如图,△ABC中,AB=3,AC=4,BC=5.△ABD,△ACE,△BCF都是等边三角形,则四边形AEFD的面积为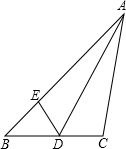 如图,在△ABC中,D是边BC上一点,AD平分∠BAC,在AB上截取AE=AC,连结DE.
如图,在△ABC中,D是边BC上一点,AD平分∠BAC,在AB上截取AE=AC,连结DE. 如图,太阳光线与地面成60°的角,照在地面的一只排球上,排球在地面的投影长是
如图,太阳光线与地面成60°的角,照在地面的一只排球上,排球在地面的投影长是