题目内容
已知双曲线y=
上有一点A(m,n),且m,n是方程t2-4t-2=0的两根,则k= ,点A到原点的距离是 .
| k |
| x |
考点:反比例函数图象上点的坐标特征,根与系数的关系
专题:
分析:(1)根据题意,根据反比例函数图象上点的特点,可得mn=k,又由一元二次方程中根与系数的关系,可得mn=-2,进而可得k的值;
(2)根据题意,m、n是方程t2-4t-2=0的两个根,结合根与系数的关系,可得m+n=4,mn=-2,又由
点A到原点的距离是:
=
,代入数据可得答案.
(2)根据题意,m、n是方程t2-4t-2=0的两个根,结合根与系数的关系,可得m+n=4,mn=-2,又由
点A到原点的距离是:
| m2+n2 |
| (m+n)2-2mn |
解答:
解:(1)根据题意,反比例函数y=
图象上有一点A,它的坐标是(m,n),
则有mn=k,
又由m、n是方程t2-4t-2=0的两个根,
则根据根与系数的关系可得mn=-2,
故k=-2;
故答案为-2.
(2)根据题意,m、n是方程t2-4t-2=0的两个根,
则m+n=4,mn=-2,
所以点A到原点的距离是:
=
=
=2
.
故答案为2
.
| k |
| x |
则有mn=k,
又由m、n是方程t2-4t-2=0的两个根,
则根据根与系数的关系可得mn=-2,
故k=-2;
故答案为-2.
(2)根据题意,m、n是方程t2-4t-2=0的两个根,
则m+n=4,mn=-2,
所以点A到原点的距离是:
| m2+n2 |
| (m+n)2-2mn |
| 42-2×(-2) |
| 5 |
故答案为2
| 5 |
点评:本题主要考查一元二次方程根与系数的关系,注意先整理变形为两根积与和的形式,再代入求值的思路.

练习册系列答案
 全优点练单元计划系列答案
全优点练单元计划系列答案
相关题目
已知点A(a+1,a-1)在双曲线y=
上,则点A的坐标是( )
| 3 |
| x |
| A、(3,1) |
| B、(3,1)或(-1,-3) |
| C、(1,3)或(-1,-3) |
| D、(-3,-1)或(-1,-3) |
下列各式与-
相加的结果可以用一个二次根式表示的是( )
| 2 |
A、
| ||
B、
| ||
C、-
| ||
D、
|

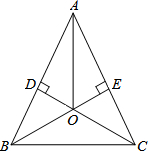 如图,AB=AC,CD⊥AB,BE⊥AC,垂足分别为点D,E,BE与CD相交于点O,连接BC,AO.求证:
如图,AB=AC,CD⊥AB,BE⊥AC,垂足分别为点D,E,BE与CD相交于点O,连接BC,AO.求证: