题目内容
17.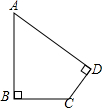 有一块土地的形状如图所示,∠B=∠D=90°,AB=20m,BC=15m,CD=7m,则这块土地的面积为234m2.
有一块土地的形状如图所示,∠B=∠D=90°,AB=20m,BC=15m,CD=7m,则这块土地的面积为234m2.
分析 连接AC,则△ABC和△ACD均为直角三角形,根据AB,BC可以求出AC,根据AC,CD可以求出AD,根据直角三角形面积计算可以求出△ABC和△ACD的面积,四边形ABCD的面积为两个直角三角形面积之和.
解答 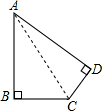 解:连接AC,将四边形分割成两个三角形,其面积为两个三角形的面积之和,
解:连接AC,将四边形分割成两个三角形,其面积为两个三角形的面积之和,
在Rt△ABC中,AC为斜边,
则AC=$\sqrt{A{B}^{2}+B{C}^{2}}$=$\sqrt{2{0}^{2}+1{5}^{2}}$=25(m),
在Rt△ACD中,AC为斜边
则AD=$\sqrt{A{C}^{2}-C{D}^{2}}$=$\sqrt{2{5}^{2}-{7}^{2}}$═24(m),
四边形ABCD面积S=$\frac{1}{2}$AB×BC+$\frac{1}{2}$AD×CD=$\frac{1}{2}$×20×25+$\frac{1}{2}$×7×24=234(m2).
答:此块地的面积为234平方米.
故答案为:234m2.
点评 本题考查了勾股定理在实际生活中的应用以及直角三角形面积计算,本题中正确的运用勾股定理计算AC是解题的关键.

练习册系列答案
 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案
相关题目
8. 如图,AB∥CD,DE⊥CE,∠1=34°,则∠DCE的度数为( )
如图,AB∥CD,DE⊥CE,∠1=34°,则∠DCE的度数为( )
 如图,AB∥CD,DE⊥CE,∠1=34°,则∠DCE的度数为( )
如图,AB∥CD,DE⊥CE,∠1=34°,则∠DCE的度数为( )| A. | 34° | B. | 56° | C. | 66° | D. | 54° |
5.若多项式x2+2ax+4能用完全平方公式进行因式分解,则a值为( )
| A. | 2 | B. | -2 | C. | ±2 | D. | ±4 |
 ∥
∥ ,∠1=120°,∠A=55°,则∠ACB的大小是______.
,∠1=120°,∠A=55°,则∠ACB的大小是______.
 如图,△ABC是等边三角形.
如图,△ABC是等边三角形.