题目内容
10.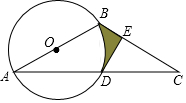 如图,⊙O的直径AB=4,∠BAC=30°,AC交⊙O于D,D是AC的中点.
如图,⊙O的直径AB=4,∠BAC=30°,AC交⊙O于D,D是AC的中点.(1)过点D作DE⊥BC,垂足为E,求证:直线DE是⊙O的切线;
(2)求$\widehat{BD}$与线段DE、BE围成的阴影面积.
分析 (1)连接OD,易证DO是△ABC的中位线,从而可知OD∥BC,所以∠EDO=∠CED,由于DE⊥BC,从而可知DE是⊙O的切线;
(2)连接BD,分别求出四边形OBED与扇形OBD的面积,然后即可求出阴影部分面积.
解答 (1)证明:连接OD.
∵D是AC的中点,O是AB的中点,
∴DO是△ABC的中位线,
∴OD∥BC,则∠EDO=∠CED
又∵DE⊥BC,
∴∠CED=90°,
∴∠EDO=∠CED=90°
∴OD⊥DE
∴DE是⊙O的切线,
(2)连接BD
∵AB是直径
∴∠ADB=90°
∵∠BAC=30°,AB=4
∴∠BOD=2∠ABD=60°
∵OB=OD
∴△OBD是等边三角形
∴∠ODB=∠BOD=60°,OB=OD=BD=2
∵∠EDO=90°
∴∠BDE=30°
∴在Rt△BDE中 BE=1,DE=$\sqrt{3}$
∴S阴=S四边形ODEB-S扇形OBD=$\frac{(1+2)\sqrt{3}}{2}$-$\frac{60π{×2}^{2}}{360}$=$\frac{3\sqrt{3}}{2}$-$\frac{2π}{3}$
答:阴影面积为$\frac{3\sqrt{3}}{2}$-$\frac{2π}{3}$
点评 本题考查圆的综合问题,涉及圆周定理,等边三角形的性质与判定,切线的判定,扇形面积公式,综合程度较高,属于中等题型.

练习册系列答案
相关题目
5. 如图,在正方形ABCD中,AB=6,分别以A、B、C、D为圆心,以正方形的边长为半径画弧,弧的交点设为E,F,G,H,则图中阴影部分的面积是$\frac{3+π-3\sqrt{3}}{3}$a2.
如图,在正方形ABCD中,AB=6,分别以A、B、C、D为圆心,以正方形的边长为半径画弧,弧的交点设为E,F,G,H,则图中阴影部分的面积是$\frac{3+π-3\sqrt{3}}{3}$a2.
 如图,在正方形ABCD中,AB=6,分别以A、B、C、D为圆心,以正方形的边长为半径画弧,弧的交点设为E,F,G,H,则图中阴影部分的面积是$\frac{3+π-3\sqrt{3}}{3}$a2.
如图,在正方形ABCD中,AB=6,分别以A、B、C、D为圆心,以正方形的边长为半径画弧,弧的交点设为E,F,G,H,则图中阴影部分的面积是$\frac{3+π-3\sqrt{3}}{3}$a2.
15.计算结果为a6的是( )
| A. | a3+a3 | B. | a2•a3 | C. | (a3)2 | D. | a12÷a2 |
19.已知∠A和∠B互余,∠A比∠B大10°,设∠A、∠B的度数分别为x°、y°,下列方程组在符合题意的是( )
| A. | $\left\{\begin{array}{l}{x+y=90}\\{x=y+10}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{x+y=90}\\{x=y-10}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{x+y=180}\\{x=y-10}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{x+y=180}\\{x=y+10}\end{array}\right.$ |
 如图,四边形ABCD是⊙O的内接四边形,⊙O的半径为2,弧AC的长为π,则∠ADC的大小是135°.
如图,四边形ABCD是⊙O的内接四边形,⊙O的半径为2,弧AC的长为π,则∠ADC的大小是135°.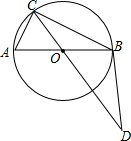 如图,AB是⊙O的直径,C为⊙O上一点,点D在CO的延长线上,连接BD,已知BC=BD,AB=4,BC=2$\sqrt{3}$.
如图,AB是⊙O的直径,C为⊙O上一点,点D在CO的延长线上,连接BD,已知BC=BD,AB=4,BC=2$\sqrt{3}$.