题目内容
12.D、E分别是△ABC的AB、AC边的中点,延长DE至F,使EF=DE,连接CF,则△CEF与四边形BCED的面积之比为( )| A. | 1:3 | B. | 2:3 | C. | 1:4 | D. | 2:5 |
分析 利用SAS得到三角形ADE与三角形CFE全等,利用全等三角形面积相等得到两三角形面积相等,由DE为三角形ABC中位线,利用中位线定理得到DE与BC平行,且等于BC的一半,进而确定出三角形ADE与三角形ABC相似,且相似比为1:2,面积之比为1:4,即可确定出所求面积之比.
解答 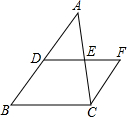 解:在△ADE和△CFE中,
解:在△ADE和△CFE中,
$\left\{\begin{array}{l}{AE=CE}\\{∠AED=∠CEF}\\{DE=FE}\end{array}\right.$,
∴△ADE≌△CFE(SAS),
∴S△ADE=S△CFE,
∵DE为△ABC的中位线,
∴DE∥BC,DE=$\frac{1}{2}$BC,
∴△ADE∽△ABC,且相似比为1:2,
∴S△ADE=$\frac{1}{4}$S△ABC,即S△CFE=$\frac{1}{4}$S△ABC,
则△CEF与四边形BCED的面积之比为1:3,
故选A
点评 此题考查了相似三角形的判定与性质,以及三角形中位线定理,熟练掌握相似三角形的判定与性质是解本题的关键.

练习册系列答案
 超能学典应用题题卡系列答案
超能学典应用题题卡系列答案
相关题目
20.下列关系式中,是用含x的代数式表示y的是( )
| A. | y=2x-3y | B. | x=2-3y | C. | -y=2x-1 | D. | y=x |
7. 如图,点A,B,C在⊙O上,CO的延长线交AB于点D,∠B=40°,∠ADC=110°,则∠A的度数为( )
如图,点A,B,C在⊙O上,CO的延长线交AB于点D,∠B=40°,∠ADC=110°,则∠A的度数为( )
 如图,点A,B,C在⊙O上,CO的延长线交AB于点D,∠B=40°,∠ADC=110°,则∠A的度数为( )
如图,点A,B,C在⊙O上,CO的延长线交AB于点D,∠B=40°,∠ADC=110°,则∠A的度数为( )| A. | 50° | B. | 55° | C. | 60° | D. | 65° |
17.下列选项正确的是( )
| A. | -|-2|<-3 | B. | 绝对值小于4的正数有-4,-3,-2,-1 | ||
| C. | (-2)n<0(n为正整数) | D. | 若a2=(-2)2,则a=±2 |
4.若代数式3x2+ax+4-(bx2+2x)的值与字母x无关,则$\frac{1}{2}$a2-$\frac{1}{3}$b的值为( )
| A. | -1 | B. | 1 | C. | -$\frac{23}{6}$ | D. | $\frac{23}{6}$ |
1.下列四个命题中,它的逆命题成立的是( )
| A. | 如果x=y,那么|x|=|y| | B. | 对顶角相等 | ||
| C. | 全等三角形的对应角相等 | D. | 直角三角形的两个锐角互余 |
 已知:如图,平面直角坐标系中,A(0,8),B(0,4),点C是x轴上一点,点D为OC的中点.
已知:如图,平面直角坐标系中,A(0,8),B(0,4),点C是x轴上一点,点D为OC的中点. 如图,△ABC,∠A=90°,AB=AC,△ABC的面积为12,则BC的长为4$\sqrt{3}$.
如图,△ABC,∠A=90°,AB=AC,△ABC的面积为12,则BC的长为4$\sqrt{3}$. 一个正方体的每个面都写有一个汉字,其平面展开图如图所示,那么在该正方体中,和“我”的对面上所写的字是丽.
一个正方体的每个面都写有一个汉字,其平面展开图如图所示,那么在该正方体中,和“我”的对面上所写的字是丽.