题目内容
13. 如图,矩形ABCD中,已知AB=6,BC=8,BD的垂直平分线交AD于点E,交BC于点F,则△BOF的面积为$\frac{75}{8}$.
如图,矩形ABCD中,已知AB=6,BC=8,BD的垂直平分线交AD于点E,交BC于点F,则△BOF的面积为$\frac{75}{8}$.
分析 根据矩形的性质和勾股定理求出BD,证明△BOF∽△BCD,根据相似三角形的性质得到比例式,求出BF,根据勾股定理求出OF,根据三角形的面积公式计算即可.
解答 解:∵四边形ABCD是矩形,
∴∠A=90°,又AB=6,AD=BC=8,
∴BD=$\sqrt{A{B}^{2}+A{D}^{2}}$=10,
∵EF是BD的垂直平分线,
∴OB=OD=5,∠BOF=90°,又∠C=90°,
∴△BOF∽△BCD,
∴$\frac{BO}{BC}$=$\frac{BF}{BD}$,即$\frac{5}{8}$=$\frac{BF}{10}$,
解得,BF=$\frac{25}{4}$,
则OF=$\sqrt{B{F}^{2}-O{B}^{2}}$=$\frac{15}{4}$,
则△BOF的面积=$\frac{1}{2}$×OF×OB=$\frac{75}{8}$,
故答案为:$\frac{75}{8}$.
点评 本题考查的是矩形的性质、线段垂直平分线的性质以及勾股定理的应用,掌握矩形的四个角是直角、对边相等以及线段垂直平分线的定义是解题的关键.

练习册系列答案
相关题目
3.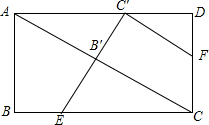 如图,在矩形ABCD中,点E在BC上,将△ABE沿AE翻折,点B恰好落在对角线AC上的B′处,点F在CD上,将△ECF沿EF翻折,点C恰好落在AD上的C′处,若E、B′C′三点共线,则$\frac{CF}{AB}$=( )
如图,在矩形ABCD中,点E在BC上,将△ABE沿AE翻折,点B恰好落在对角线AC上的B′处,点F在CD上,将△ECF沿EF翻折,点C恰好落在AD上的C′处,若E、B′C′三点共线,则$\frac{CF}{AB}$=( )
 如图,在矩形ABCD中,点E在BC上,将△ABE沿AE翻折,点B恰好落在对角线AC上的B′处,点F在CD上,将△ECF沿EF翻折,点C恰好落在AD上的C′处,若E、B′C′三点共线,则$\frac{CF}{AB}$=( )
如图,在矩形ABCD中,点E在BC上,将△ABE沿AE翻折,点B恰好落在对角线AC上的B′处,点F在CD上,将△ECF沿EF翻折,点C恰好落在AD上的C′处,若E、B′C′三点共线,则$\frac{CF}{AB}$=( )| A. | $\frac{\sqrt{2}}{3}$ | B. | $\frac{2}{3}$ | C. | $\frac{\sqrt{2}}{2}$ | D. | $\frac{3}{4}$ |
4.下列说法正确的是( )
| A. | 掷一枚质地均匀的正方体骰子,骰子停止转动后,5点朝上是必然事件 | |
| B. | 审查书稿中有哪些学科性错误适合用抽样调查法 | |
| C. | 甲乙两人在相同条件下各射击10次,他们的成绩的平均数相同,方差分别是S甲2=0.4,S乙2=0.6,则甲的射击成绩较稳定 | |
| D. | 掷两枚质地均匀的硬币,“两枚硬币都是正面朝上”这一事件发生的概率为$\frac{1}{2}$ |
8.一元二次方程(x+1)2-2(x-1)2=7的根的情况是( )
| A. | 无实数根 | B. | 有一正根一负根 | C. | 有两个正根 | D. | 有两个负根 |
18. 如图,一扇形纸扇完全打开后,外侧两竹条AB和AC的夹角为120°,AB长为25cm,贴纸部分的宽BD为15cm,若纸扇两面贴纸,则贴纸的面积为( )
如图,一扇形纸扇完全打开后,外侧两竹条AB和AC的夹角为120°,AB长为25cm,贴纸部分的宽BD为15cm,若纸扇两面贴纸,则贴纸的面积为( )
 如图,一扇形纸扇完全打开后,外侧两竹条AB和AC的夹角为120°,AB长为25cm,贴纸部分的宽BD为15cm,若纸扇两面贴纸,则贴纸的面积为( )
如图,一扇形纸扇完全打开后,外侧两竹条AB和AC的夹角为120°,AB长为25cm,贴纸部分的宽BD为15cm,若纸扇两面贴纸,则贴纸的面积为( )| A. | 175πcm2 | B. | 350πcm2 | C. | $\frac{800}{3}$πcm2 | D. | 150πcm2 |
5.成都地铁自开通以来,发展速度不断加快,现已成为成都市民主要出行方式之一.今年4月29日成都地铁安全运输乘客约181万乘次,又一次刷新客流纪录,这也是今年以来第四次客流纪录的刷新,用科学记数法表示181万为( )
| A. | 18.1×105 | B. | 1.81×106 | C. | 1.81×107 | D. | 181×104 |
3.为了绿化校园,30名学生共种78棵树苗.其中男生每人种3棵,女生每人种2棵,该班男生有x人,女生有y人.根据题意,所列方程组正确的是( )
| A. | $\left\{\begin{array}{l}{x+y=78}\\{3x+2y=30}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{x+y=78}\\{2x+3y=30}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{x+y=30}\\{2x+3y=78}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{x+y=30}\\{3x+2y=78}\end{array}\right.$ |
 如图,△ABC的外接圆O的半径为2,∠C=40°,则$\widehat{AB}$的长是$\frac{8}{9}$π.
如图,△ABC的外接圆O的半径为2,∠C=40°,则$\widehat{AB}$的长是$\frac{8}{9}$π.