题目内容
一次函数y=a x+b(a>0)、二次函数y=ax2+bx和反比例函数y=
x+b(a>0)、二次函数y=ax2+bx和反比例函数y=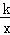
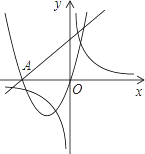
 (k≠0)在同一直角坐标系中的图象如图所示,A点的坐标为(﹣2,0),则下列结论中,正确的是( )
(k≠0)在同一直角坐标系中的图象如图所示,A点的坐标为(﹣2,0),则下列结论中,正确的是( )


A.a>b>0 B.a>k>0 C.b=2a+k D.a=b+k
B
【解析】
试题分析:根据函数图象知,由一次函数图象所在的象限可以确定a、b的符号,且直线与抛物线均经过点A,所以把点A的坐标代入一次函数或二次函数可以求得b=2a, k的符号可以根据
k的符号可以根据 双曲线所在的象限进行判定.
双曲线所在的象限进行判定.
解: ∵根据图示知,一次函数与二次函数的交点A
∵根据图示知,一次函数与二次函数的交点A 的坐标为(﹣2,0),
的坐标为(﹣2,0),
∴﹣2a+b=0,
∴b=2a.

故本选项错误;
B、观察二次函数y=ax2+bx和反比例函数y=
 (k≠0)图象知,当x=﹣
(k≠0)图象知,当x=﹣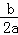
 =﹣
=﹣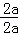
 =﹣1时,y=﹣k>﹣
=﹣1时,y=﹣k>﹣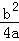
 =﹣
=﹣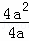
 =﹣a,即k<a,
=﹣a,即k<a,
∵a>0,k>0,
∴a>k>0.
故本选项正确;

故选B.

点评:本题综合考查了一次函数、二次函数以及反比例函数的图象 .解题的关键是会读图,从图中提取有用的信息.
.解题的关键是会读图,从图中提取有用的信息.

练习册系列答案
 全能测控期末小状元系列答案
全能测控期末小状元系列答案
相关题目
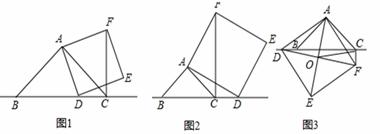
 ,对角线AE,DF相交于点O,连接OC 求OC的长度.
,对角线AE,DF相交于点O,连接OC 求OC的长度.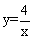 图象上,点B在反比例函数
图象上,点B在反比例函数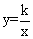 (k≠0)的图象上,CB∥x轴,BD∥AO,若CA=
(k≠0)的图象上,CB∥x轴,BD∥AO,若CA=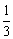 CB,则双曲线
CB,则双曲线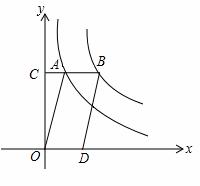
 bx+1与x轴只有一个交点,且过点A(m,n),B(m+4,n),则n=
bx+1与x轴只有一个交点,且过点A(m,n),B(m+4,n),则n=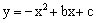 的顶点为D(﹣1,4),与
的顶点为D(﹣1,4),与 轴交于点C(0,3),与
轴交于点C(0,3),与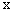 轴交于A,B两点(点A在点B的左侧)。
轴交于A,B两点(点A在点B的左侧)。
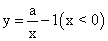 的图象如图,那么关于x的分式方程
的图象如图,那么关于x的分式方程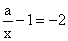 的解是【 】
的解是【 】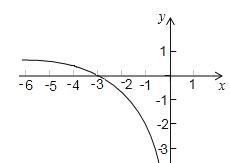
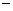 1 B.x=
1 B.x=

 自行车和摩托车行驶过程的函数解析式(不要求写出自变量的取值范围);
自行车和摩托车行驶过程的函数解析式(不要求写出自变量的取值范围); 或不等式(不要化简,也不要求解):①自行车行驶在摩托车前面;②自行车与摩托车相遇;③自行车行驶在摩托车后面.
或不等式(不要化简,也不要求解):①自行车行驶在摩托车前面;②自行车与摩托车相遇;③自行车行驶在摩托车后面. ABCD,对角线AC与BD相交于点O,点P在边AD上,过点P分别作PE⊥AC
ABCD,对角线AC与BD相交于点O,点P在边AD上,过点P分别作PE⊥AC 、PF⊥BD,垂足分别为E、F。
、PF⊥BD,垂足分别为E、F。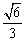 PE,PE=
PE,PE= ,EO=1,求∠EPF的度数;
,EO=1,求∠EPF的度数; -4,求BC的长。
-4,求BC的长。
 ,并求出使
,并求出使