题目内容
7.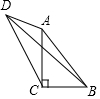 在Rt△ABC中,∠ACB=90°,点D为△ABC外一点,连接AD、CD、∠ADC=45°,连接BD,∠DBC=2∠ADB,AB=5,BD=7,则BC=3或4.
在Rt△ABC中,∠ACB=90°,点D为△ABC外一点,连接AD、CD、∠ADC=45°,连接BD,∠DBC=2∠ADB,AB=5,BD=7,则BC=3或4.
分析 作DH⊥AD交BC的延长线于H,连接AH.首先证明BH=BD=7,△ACH是等腰直角三角形,设BC=a,则AC=7-a,在Rt△ACB中,利用勾股定理即可解决问题.
解答 解:作DH⊥AD交BC的延长线于H,连接AH.
设∠ADB=x,则∠DBH=2x,∠BDH=90°-x,
∴∠BHD=180°-2x-(90°-x)=90°-x.
∴∠BHD=∠BDH,
∴BH=BD=7,
∵∠ADH=∠ACH=90°,
∴A、D、H、C四点共圆,
∴∠AHC=∠ADC=45°,
∴AC=CH,设BC=a,
则CH=AC=7-a,
在Rt△ACB中,∵AC2+BC2=AB2,
∴52=a2+(7-a)2,
解得a=4或3,
∴BC的值为3或4.
故答案为3或4.
点评 本题考查勾股定理、等腰三角形的判定和性质、等腰直角三角形的判定和性质、四点共圆等知识,解题的关键是学会添加辅助线,构造特殊三角形解决问题,题目比较难.

练习册系列答案
 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案
相关题目
5. 有研究表明,长时间看手机会引发眼睛模糊、颈椎炎、记忆力下降等健康问题.某社区为了解居民平均每天看手机的时间t,随机抽取了社区内200人进行了抽查,调查数据统计如图表.
有研究表明,长时间看手机会引发眼睛模糊、颈椎炎、记忆力下降等健康问题.某社区为了解居民平均每天看手机的时间t,随机抽取了社区内200人进行了抽查,调查数据统计如图表.
(1)平均每天看手机的时间不小于2小时的人数等于15人;
(2)如果按t各个范围的人数分布情况制作扇形统计图,那么表示平均每天看手机的时间小于0.5小时的扇形圆心角的度数n等于86.4°;
(3)若该社区共有居民1600人,估计平均每天看手机的时间小于1小时的人有多少?
 有研究表明,长时间看手机会引发眼睛模糊、颈椎炎、记忆力下降等健康问题.某社区为了解居民平均每天看手机的时间t,随机抽取了社区内200人进行了抽查,调查数据统计如图表.
有研究表明,长时间看手机会引发眼睛模糊、颈椎炎、记忆力下降等健康问题.某社区为了解居民平均每天看手机的时间t,随机抽取了社区内200人进行了抽查,调查数据统计如图表.(1)平均每天看手机的时间不小于2小时的人数等于15人;
(2)如果按t各个范围的人数分布情况制作扇形统计图,那么表示平均每天看手机的时间小于0.5小时的扇形圆心角的度数n等于86.4°;
(3)若该社区共有居民1600人,估计平均每天看手机的时间小于1小时的人有多少?
| 平均每天看手机的时间t(小时) | 人数(人) | 比例(%) |
| t<0.5 | ||
| 0.5≤t<1 | 38 | |
| 1≤t<1.5 | 33% | |
| 1.5≤t<2 | 33 | |
| t≥2 | 15 |
12.矩形ABCD中,两条对角线的长为6cm,且一夹角为60°,则矩形ABCD的周长为( )
| A. | 6+6$\sqrt{3}$ | B. | 6$\sqrt{3}$+6$\sqrt{2}$ | C. | 12 | D. | 18 |
19.式子$\sqrt{2}$的值( )
| A. | 在0到1之间 | B. | 在1到2之间 | C. | 在2到3之间 | D. | 等于4 |
 如图是边长为10cm的正方形铁片,过两个顶点剪掉一个三角形,以下四种剪法中,裁剪线长度所标的数据(单位:cm)不正确的是( )
如图是边长为10cm的正方形铁片,过两个顶点剪掉一个三角形,以下四种剪法中,裁剪线长度所标的数据(单位:cm)不正确的是( )



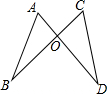 如图,线段AD、BC相交于点O,连接AB、CD.下列条件:①AB=CD,AO=CO;②∠A=∠C,AO=CO;③AO=CO,BO=DO;④∠B=∠D,AB=CD;⑤∠B=∠D,∠A=∠C;从中任选一组能得出△ABO≌△CDO的概率是$\frac{3}{5}$.
如图,线段AD、BC相交于点O,连接AB、CD.下列条件:①AB=CD,AO=CO;②∠A=∠C,AO=CO;③AO=CO,BO=DO;④∠B=∠D,AB=CD;⑤∠B=∠D,∠A=∠C;从中任选一组能得出△ABO≌△CDO的概率是$\frac{3}{5}$.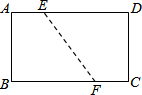 如图,已知矩形ABCD的边AB=3,BC=9,将其折叠,使得点D与点B重合,折叠后折痕EF的长是$\sqrt{10}$.
如图,已知矩形ABCD的边AB=3,BC=9,将其折叠,使得点D与点B重合,折叠后折痕EF的长是$\sqrt{10}$.