题目内容
17.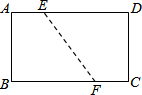 如图,已知矩形ABCD的边AB=3,BC=9,将其折叠,使得点D与点B重合,折叠后折痕EF的长是$\sqrt{10}$.
如图,已知矩形ABCD的边AB=3,BC=9,将其折叠,使得点D与点B重合,折叠后折痕EF的长是$\sqrt{10}$.
分析 设BD于EF交于点O,则O是BD的中点,易证△ABD∽△OED,根据相似三角形的对应的边的比相等,即可求得OE的长,再根据EF=2OE即可求解.
解答 解:设BD于EF交于点O,则O是BD的中点.
在直角△ABD中,BD=$\sqrt{A{B}^{2}+A{D}^{2}}$=$\sqrt{{9}^{2}+{3}^{2}}$=3 $\sqrt{10}$cm;
则OD=$\frac{3}{2}$$\sqrt{10}$.
∵B、D关于EF对称,
∴∠EOD=90°,
又∵矩形ABCD中,∠A=90°,
∴∠A=∠EOD=90°.
在△ABD于△OED中,∠A=∠EOD=90°,∠ADB=∠ODE,
∴△ABD∽△OED.
∴$\frac{OE}{AB}$=$\frac{OD}{AD}$,
∴OE=$\frac{OD}{AD}$•AB=$\frac{\sqrt{10}}{2}$cm.
∴EF=2OE=$\sqrt{10}$cm.
点评 本题考查了对称的性质以及相似三角形的判定与性质,正确证明△ABD∽△OED是解题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
9. 如图,?ABCD的周长为20,∠BAD的平分线AE交BC与点E,若BE=2,则CE等于( )
如图,?ABCD的周长为20,∠BAD的平分线AE交BC与点E,若BE=2,则CE等于( )
 如图,?ABCD的周长为20,∠BAD的平分线AE交BC与点E,若BE=2,则CE等于( )
如图,?ABCD的周长为20,∠BAD的平分线AE交BC与点E,若BE=2,则CE等于( )| A. | 2 | B. | 4 | C. | 6 | D. | 8 |
7. 如图,点A在直线l1上,点B,C分别在直线l2上,AB⊥l2于点B,AC⊥l1于点A,AB=4,AC=5,则下列说法正确的是( )
如图,点A在直线l1上,点B,C分别在直线l2上,AB⊥l2于点B,AC⊥l1于点A,AB=4,AC=5,则下列说法正确的是( )
 如图,点A在直线l1上,点B,C分别在直线l2上,AB⊥l2于点B,AC⊥l1于点A,AB=4,AC=5,则下列说法正确的是( )
如图,点A在直线l1上,点B,C分别在直线l2上,AB⊥l2于点B,AC⊥l1于点A,AB=4,AC=5,则下列说法正确的是( )| A. | 点B到直线l1的距离等于4 | B. | 点A到直线l2的距离等于5 | ||
| C. | 点B到直线l1的距离等于5 | D. | 点C到直线l1的距离等于5 |
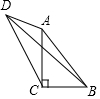 在Rt△ABC中,∠ACB=90°,点D为△ABC外一点,连接AD、CD、∠ADC=45°,连接BD,∠DBC=2∠ADB,AB=5,BD=7,则BC=3或4.
在Rt△ABC中,∠ACB=90°,点D为△ABC外一点,连接AD、CD、∠ADC=45°,连接BD,∠DBC=2∠ADB,AB=5,BD=7,则BC=3或4.