题目内容
18.对于任意实数x,多项式x2-5x+8的值是一个( )| A. | 非负数 | B. | 正数 | C. | 负数 | D. | 无法确定 |
分析 根据完全平方公式,将x2-5x+8转化为完全平方的形式,再进一步判断.
解答 解:x2-5x+8=x2-5x+$\frac{25}{4}$+$\frac{7}{4}$=(x-$\frac{5}{2}$)2+$\frac{7}{4}$,
任意实数的平方都是非负数,其最小值是0,
所以(x-$\frac{5}{2}$)2+$\frac{7}{4}$的最小值是$\frac{7}{4}$,
故多项式x2-5x+8的值是一个正数,
故选:B.
点评 本题考查了配方法的应用和非负数的性质.任意实数的平方和绝对值都具有非负性,灵活运用这一性质是解决此类问题的关键.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
13.某市2012年国内生产总值(GDP)比2011年增长了12%,由于受到国际金融危机的影响,预计2013年比2012年增长7%.若这两年GDP平均增长率为x%,则x%满足的关系是( )
| A. | 12%+7%=x% | B. | (1+12%)(1+7%)=2(1+x%) | C. | 12%+7%=2•x% | D. | (1+12%)(1+7%)=(1+x%)2 |
10.若a+b+c=2015,则抛物线y=ax2+bx+c必定经过的点是( )
| A. | (-1,-2015) | B. | (1,2015) | C. | (-1,2015) | D. | (1,-2015) |
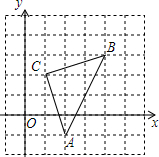 如图,直角坐标系中,△ABC的顶点都在网格点上,其中,C点坐标为(1,2),
如图,直角坐标系中,△ABC的顶点都在网格点上,其中,C点坐标为(1,2),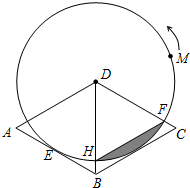 如图,在菱形ABCD中,∠A=60°,以点D为圆心的⊙D与边AB相切于点E.
如图,在菱形ABCD中,∠A=60°,以点D为圆心的⊙D与边AB相切于点E.