��Ŀ����
7��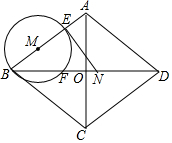 ��ͼ������ABCD�У��Խ���AC��BD�ཻ�ڵ�O��AC=12cm��BD=16cm������N�ӵ�D���������߶�DB��2cm/s���ٶ����B�˶���ͬʱ����M�ӵ�B���������߶�BA��1cm/s���ٶ����A�˶���������һ������ֹͣ�˶�ʱ��һ������Ҳ��ֹ֮ͣ�����˶�ʱ��Ϊt��s����t��0�����Ե�MΪԲ�ģ�MB��Ϊ�뾶�ġ�M������BA���߶�BD�ֱ��ڵ�E��F������EN��
��ͼ������ABCD�У��Խ���AC��BD�ཻ�ڵ�O��AC=12cm��BD=16cm������N�ӵ�D���������߶�DB��2cm/s���ٶ����B�˶���ͬʱ����M�ӵ�B���������߶�BA��1cm/s���ٶ����A�˶���������һ������ֹͣ�˶�ʱ��һ������Ҳ��ֹ֮ͣ�����˶�ʱ��Ϊt��s����t��0�����Ե�MΪԲ�ģ�MB��Ϊ�뾶�ġ�M������BA���߶�BD�ֱ��ڵ�E��F������EN����1����BF�ij����ú���t�Ĵ���ʽ��ʾ���������t��ȡֵ��Χ��
��2����tΪ��ֵʱ���߶�EN���M���У�
��3������M���߶�ENֻ��һ�������㣬��t��ȡֵ��Χ��
���� ��1������MF��ֻҪ֤��MF��AD���ɵ�$\frac{BM}{BA}$=$\frac{BF}{BD}$����$\frac{t}{10}$=$\frac{BF}{16}$���ⷽ�̼��ɣ�
��2�����߶�EN���M����ʱ����֪��BEN�ס�BOA���ɵ�$\frac{BE}{OB}$=$\frac{BN}{AB}$����$\frac{2t}{8}$=$\frac{16-2t}{10}$���ⷽ�̼��ɣ�
��3���������֪����0��t��$\frac{32}{7}$��$\frac{40}{9}$��t��8ʱ����M���߶�ENֻ��һ�������㣻
��� �⣺��1������MF��
���ı���ABCD�����Σ�
��AB=AD��AC��BD��OA=OC=6��OB=OD=8��
��Rt��AOB��AB=$\sqrt{{6}^{2}+{8}^{2}}$=10��
��MB=MF��AB=AD��
���ABD=��ADB=��MFB��
��MF��AD��
��$\frac{BM}{BA}$=$\frac{BF}{BD}$��
��$\frac{t}{10}$=$\frac{BF}{16}$��
��BF=$\frac{8}{5}$t��0��t��8����
��2�����߶�EN���M����ʱ����֪��BEN�ס�BOA��
��$\frac{BE}{OB}$=$\frac{BN}{AB}$��
��$\frac{2t}{8}$=$\frac{16-2t}{10}$��
��t=$\frac{32}{9}$��
��t=$\frac{32}{9}$sʱ���߶�EN���M���У�
��3���������֪����0��t��$\frac{32}{9}$ʱ����M���߶�ENֻ��һ�������㣮
����N�ڡ�M�ڲ�ʱ��Ҳ������������F��N�غ�ʱ$\frac{8}{5}$t+2t=16�����t=$\frac{40}{9}$��s����
��$\frac{40}{9}$��t��8ʱ����M���߶�ENֻ��һ�������㣬
��������������������t�ķ�ΧΪ0��t��$\frac{32}{9}$��$\frac{40}{9}$��t��8��
���� ���⿼��Բ�ۺ��⡢���ε����ʡ����ߵ����ʡ����ɶ�����ƽ���߷��߶γɱ���������֪ʶ������Ĺؼ������������ѧ֪ʶ������⣮ѧ���ù������̵�˼��˼�����⣮�����п�ѹ���⣮

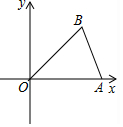 ��ͼ����ƽ��ֱ������ϵxOy�У���֪��A��$\sqrt{2}$��0����B��1��1������ƽ�Ƶ�A����C��ʹ�Ե�O��A��C��BΪ������ı��������Σ�����ȷ��ƽ�Ʒ����ǣ�������
��ͼ����ƽ��ֱ������ϵxOy�У���֪��A��$\sqrt{2}$��0����B��1��1������ƽ�Ƶ�A����C��ʹ�Ե�O��A��C��BΪ������ı��������Σ�����ȷ��ƽ�Ʒ����ǣ�������| A�� | ����ƽ��1����λ��������ƽ��1����λ | |
| B�� | ����ƽ�ƣ�2$\sqrt{2}$-1������λ��������ƽ��1����λ | |
| C�� | ����ƽ��$\sqrt{2}$����λ��������ƽ��1����λ | |
| D�� | ����ƽ��1����λ��������ƽ��1����λ |
| A�� | ���� | B�� | ƽ���� | C�� | ���� | D�� | ��λ�� |
| A�� | a5b5 | B�� | a4b5 | C�� | ab5 | D�� | a5b6 |
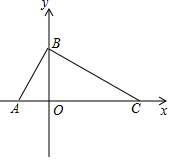 ��ͼ����ƽ��ֱ������ϵ�У���A��-1��0����B��0��2������C��x���ϣ��ҡ�ABC=90�㣮
��ͼ����ƽ��ֱ������ϵ�У���A��-1��0����B��0��2������C��x���ϣ��ҡ�ABC=90�㣮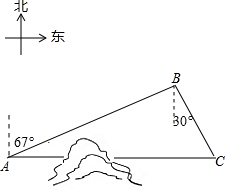 ��ͼ��C����A�ص������������д�ɽ�������A�ص�C��������B�أ���֪B��λ��A�ر�ƫ��67�㷽����A��520km��C��λ��B����ƫ��30�㷽������ͨ��ɽ��������������ֱ���������A�ص�C��֮�������·�ij������������������
��ͼ��C����A�ص������������д�ɽ�������A�ص�C��������B�أ���֪B��λ��A�ر�ƫ��67�㷽����A��520km��C��λ��B����ƫ��30�㷽������ͨ��ɽ��������������ֱ���������A�ص�C��֮�������·�ij������������������


