题目内容
某公司生产A种产品,它的成本是2元/件,售价是3元/件,年销售量为10万件.为了获得更好的效益,公司准备拿出一定的资金做广告,根据经验,每年投入的广告费是x万元,产品的年销售量将是原销售量的y倍,且y与x之间满足我们学过的三种函数(即一次函数、反比例函数和二次函数)关系中的一种,它们的关系如下表:
(1)求y与x的函数关系式不要求写出自变量的取值范围;
(2)如果把利润看作是销售总额减去成本费用和广告费用,试求出年利润S(万元)与广告费用x(万元)的函数关系式;
(3)如果公司年投入的广告费不低于1万元且不高于3万元,问广告费在什么范围内,公司获得的年利润随广告费的增大而增大?
| x(万元) | 0 | 1 | 2 | … |
| y | 1 | 1.5 | 1.8 | … |
(2)如果把利润看作是销售总额减去成本费用和广告费用,试求出年利润S(万元)与广告费用x(万元)的函数关系式;
(3)如果公司年投入的广告费不低于1万元且不高于3万元,问广告费在什么范围内,公司获得的年利润随广告费的增大而增大?
考点:二次函数的应用
专题:
分析:(1)二次函数的解析式为y=ax2+bx+c,利用表格数据,即可求出y与x之间的函数关系式;
(2)根据利润看作是销售总额减去成本费和广告费,可得结论;
(3)利用配方法,结合x的取值范围,可求最值.
(2)根据利润看作是销售总额减去成本费和广告费,可得结论;
(3)利用配方法,结合x的取值范围,可求最值.
解答:解:(1)设二次函数的解析式为y=ax2+bx+c.
由关系表,得
,
解得
,
∴函数的解析式为y=-
x2+
x+1.
(2)根据题意,得S=10y(3-2)-x=-x2+5x+10
(3)S=-x2+5x+10=-(x-
)2+
,
∵1≤x≤3,
∴当1≤x≤2.5时,S随x的增大而增大.
故当年广告费为1~2.5万元之间,公司获得的年利润随广告费的增大而增大.
由关系表,得
|
解得
|
∴函数的解析式为y=-
| 1 |
| 10 |
| 3 |
| 5 |
(2)根据题意,得S=10y(3-2)-x=-x2+5x+10
(3)S=-x2+5x+10=-(x-
| 5 |
| 2 |
| 65 |
| 4 |
∵1≤x≤3,
∴当1≤x≤2.5时,S随x的增大而增大.
故当年广告费为1~2.5万元之间,公司获得的年利润随广告费的增大而增大.
点评:本题考查的是二次函数综合题,涉及到函数模型的建立,配方法的运用的知识,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
相关题目
已知关于x的方程2x+a=5x-4的解是x=-2,则a的值是( )
| A、-18 | B、-10 |
| C、-6 | D、-2 |
 如图,已知正方形ABCD的边长为4,点E、F分别在边AB,BC上,且AE=BF=1,则OC=
如图,已知正方形ABCD的边长为4,点E、F分别在边AB,BC上,且AE=BF=1,则OC=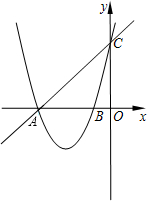 如图,在平面直角坐标系内,已知直线y=x+4与x轴、y轴分别相交于点A和点C,抛物线y=x2+kx+k-1图象过点A和点C,抛物线与x轴的另一交点是B,
如图,在平面直角坐标系内,已知直线y=x+4与x轴、y轴分别相交于点A和点C,抛物线y=x2+kx+k-1图象过点A和点C,抛物线与x轴的另一交点是B, 用圆规、直尺作图,不写作法,但要保留作图痕迹.在一块三角形废料上,要裁下一个圆形的材料,并且要尽可能的充分利用好原三角形废料,请画出这个圆形.
用圆规、直尺作图,不写作法,但要保留作图痕迹.在一块三角形废料上,要裁下一个圆形的材料,并且要尽可能的充分利用好原三角形废料,请画出这个圆形.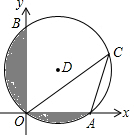 如图,在平面直角坐标系中,已知⊙D经过原点O,与x轴、y轴分别交于A、B两点,点B坐标为(0,2
如图,在平面直角坐标系中,已知⊙D经过原点O,与x轴、y轴分别交于A、B两点,点B坐标为(0,2 如图,AB是⊙O的直径,E是⊙O上的一点,C是弧AE的中点,若∠A=50°,则∠AOE的度数为
如图,AB是⊙O的直径,E是⊙O上的一点,C是弧AE的中点,若∠A=50°,则∠AOE的度数为