题目内容
6.天猫网某店铺销售新疆薄皮核桃,这种食品是健脑的佳品,它的成本价为每千克20元,经市场调查发现,该产品每天销售利润w(元)与销售价x(元/千克)有如下关系:w=ax2+bx-1600,当销售价为22元时,每天的销售利润为72元,当销售价为26元时,每天的销售利润为168元.(1)求该产品每天的销售利润w(元)与销售价x(元/千克)的关系式;
(2)当销售价定为每千克24元时,该产品每天的销售利润为多少元?
(3)如果该店铺的负责人想要在销售价不超过32元的情况下每天获得150元的销售利润,求销售定价应定为每千克多少元?
(4)如果物价部门规定这种产品的销售价不高于每千克29元,此店铺每天获得的最大利润为多少元?
分析 (1)根据“当销售价为22元时,每天的销售利润为72元,当销售价为26元时,每天的销售利润为168元”,用待定系数法求解析式即可;
(2)把x=24代入(1)中的函数表达式求出y的值即可;
(3)根据题意列方程求解,把不合题意的解舍去;
(4)根据二次函数的性质求出最值即可.
解答 解:(1)根据题意,得:
$\left\{\begin{array}{l}{484a+22b-1600=72}\\{676a+26b-1600=168}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{a=-2}\\{b=120}\end{array}\right.$.
∴w=-2x2+120x-1600;
(2)把x=24代入w=-2x2+120x-1600,
W=-2×242+120×24-1600=128,
当销售价定为每千克24元时,该产品每天的销售利润为128元;
(3)根据题意列方程得:
150=-2x2+120x-1600,
解得:x1=25,x2=35,
因为销售价不超过32元,
所以x=25,
所以每天获得150元的销售利润,销售定价应定为每千克25元;
(4)w=-2x2+120x-1600=-2(x-30)2+200,
当x≤30时,W随x的增大而增大,
又因为物价部门规定这种产品的销售价不高于每千克29元,
所以当x=29元时,店铺每天获得的利润最大,W最大=-2(29-30)2+200=198元.
点评 本题考查了二次函数的应用和一元二次方程的实际应用,解答本题的关键是得出W与x的函数关系式,另外要求同学们掌握配方法求最值得应用,难度一般.

练习册系列答案
 全优点练单元计划系列答案
全优点练单元计划系列答案
相关题目
13.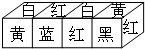 在正方体的六个面上分别涂上红、黄、蓝、白、黑、绿六种颜色,现有涂色方式完全相同的四个正方体,按照如图所示拼成一个长方体,那么涂黄、白两种颜色的面的对面分别涂有( )颜色.
在正方体的六个面上分别涂上红、黄、蓝、白、黑、绿六种颜色,现有涂色方式完全相同的四个正方体,按照如图所示拼成一个长方体,那么涂黄、白两种颜色的面的对面分别涂有( )颜色.
 在正方体的六个面上分别涂上红、黄、蓝、白、黑、绿六种颜色,现有涂色方式完全相同的四个正方体,按照如图所示拼成一个长方体,那么涂黄、白两种颜色的面的对面分别涂有( )颜色.
在正方体的六个面上分别涂上红、黄、蓝、白、黑、绿六种颜色,现有涂色方式完全相同的四个正方体,按照如图所示拼成一个长方体,那么涂黄、白两种颜色的面的对面分别涂有( )颜色.| A. | 蓝、红 | B. | 蓝、黑 | C. | 蓝、绿 | D. | 绿、白 |
13.某班有m人,体育不达标率为2%,则达标人数为( )
| A. | (1-2%)m | B. | (1+2%)m | C. | 2%m | D. | m-2% |
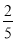 ,
, 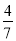 ,
, 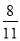 ,
, 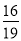 ,
, 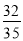 ……,小亮猜想出第六个数字是
……,小亮猜想出第六个数字是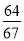 ,根据此规律,第n个数是__________.
,根据此规律,第n个数是__________. B.
B.  C.
C.  D.
D. 
