题目内容
18.如图,羽毛球运动员甲站在点O处练习发球,将球从O点正上方$\frac{3}{2}$m的P处发出,把球勘察点,其运行路线是抛物线的一部分,当球运动到最高点时,其高度为$\frac{17}{6}$m,离甲站立地点O的水平距离为4m,球网BA离O点的水平距离为5m,以O为坐标原点建立如图所示的坐标系,乙站立地点C的坐标为(m,0)(1)求出抛物线的解析式;(不写自变量的取值范围)
(2)求排球落地点N离球网的水平距离;
(3)乙原地起跳可接球的最大高度为$\frac{9}{4}$米,若乙因为接球高度不够而失球,求m的取值范围.

分析 (1)设抛物线解析式为y=a(x-4)2+$\frac{17}{6}$,将点(0,$\frac{3}{2}$)代入可得出a的值,继而得出抛物线解析式;
(2)令y=0,可得出ON的长度,由NC=ON-OA即可得出答案.
(3)先计算出刚好接到球时m的值,从而结合所给图形可得出运动员接球高度不够m的取值范围.
解答 解:(1)设抛物线解析式为y=a(x-4)2+$\frac{17}{6}$,
将点(0,$\frac{3}{2}$)代入可得:$\frac{3}{2}$=a(0-4)2+$\frac{17}{6}$,
解得:a=-$\frac{1}{12}$,
故抛物线的解析式为:y=-$\frac{1}{12}$(x-4)2+$\frac{17}{6}$;
(2)当y=0时,-$\frac{1}{12}$(x-4)2+$\frac{17}{6}$=0,
解得:x1=4-$\sqrt{34}$(舍去),x2=4+$\sqrt{34}$,
即ON=4+$\sqrt{34}$,
∵OA=5,
∴AN=$\sqrt{34}$-1(米);
(3)若运动员乙原地起跳到最大高度时刚好接到球,
此时-$\frac{1}{12}$(x-4)2+$\frac{17}{6}$=$\frac{9}{4}$,
解得:m1=4-$\sqrt{7}$,m2=4+$\sqrt{7}$,
∵运动员接球高度不够,
∴4-$\sqrt{7}$<m<4+$\sqrt{7}$,
∵OA=5,乙运动员接球时不能触网,
∴m的取值范围为:5<m<4+$\sqrt{7}$.
点评 本题考查了二次函数的应用,涉及了利用待定系数法求二次函数解析式的知识,解答本题的关键是建立直角坐标系,将实际问题转化为数学模型,难度一般.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
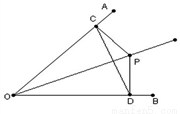
 某班共有52名同学,在校广播操比赛中排成方队,先把每位同学都进行编号,然后把各自的位置固定下来,如图,在平面直角坐标系中,每个自然数都对应着一个坐标.例如1的对应点是原点(0,0),3的对应点是(1,1),16的对应点是(-1,2).那么最后一名同学的位置对应的坐标是(4,-1),全校学生如果排成这样一个大方阵,编号是2015的学生的对应点的坐标是(12,-22).
某班共有52名同学,在校广播操比赛中排成方队,先把每位同学都进行编号,然后把各自的位置固定下来,如图,在平面直角坐标系中,每个自然数都对应着一个坐标.例如1的对应点是原点(0,0),3的对应点是(1,1),16的对应点是(-1,2).那么最后一名同学的位置对应的坐标是(4,-1),全校学生如果排成这样一个大方阵,编号是2015的学生的对应点的坐标是(12,-22).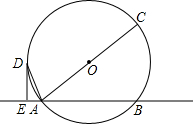 如图,直线EF交⊙O于A,B两点,AC是⊙O直径,DE是⊙O的切线,且DE⊥EF,垂足为E.
如图,直线EF交⊙O于A,B两点,AC是⊙O直径,DE是⊙O的切线,且DE⊥EF,垂足为E. 如果将点P绕定点M旋转180°后与点Q重合,那么点P与点Q关于点M对称,定点M叫做对称中心,此时,点M是线段PQ的中点,如图,在直角坐标系中,△ABO的顶点A、B、O的坐标分别为(1,0),(0,1),(0,0),点列P1、P2、P3…中的相邻两点都关于△ABO的一个顶点对称,点P1与点P2关于点A对称,点P2与点P3关于点B对称,点P3与点P4关于点O对称,点P4与点P5关于点A对称,点P5与点P6关于点B对称,点P6与点P7关于点O对称,且这些对称中心依次循环,已知点P1的坐标是(1,1),则点P2015的坐标为(1,3).
如果将点P绕定点M旋转180°后与点Q重合,那么点P与点Q关于点M对称,定点M叫做对称中心,此时,点M是线段PQ的中点,如图,在直角坐标系中,△ABO的顶点A、B、O的坐标分别为(1,0),(0,1),(0,0),点列P1、P2、P3…中的相邻两点都关于△ABO的一个顶点对称,点P1与点P2关于点A对称,点P2与点P3关于点B对称,点P3与点P4关于点O对称,点P4与点P5关于点A对称,点P5与点P6关于点B对称,点P6与点P7关于点O对称,且这些对称中心依次循环,已知点P1的坐标是(1,1),则点P2015的坐标为(1,3).