Question

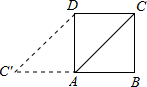如图，正方形ABCD的边长为3，将线段AC绕点A旋转后，使点C落在BA的延长线上的点C′处，则∠ADC′的余弦值为（　　）

• A、

  3

  3

• B、

  3

  2

• C、

  2

  2

• D、

  1

  2

Answer 1

考点：旋转的性质,勾股定理,正方形的性质,锐角三角函数的定义

专题：

分析：根据勾股定理得AC=3

2

，由旋转得AC′=3

2

，再根据勾股定理求得C′D，根据三角函数定义即可得出答案．

解答：解：∵正方形ABCD的边长为3，
∴AC=3

2

，
∵线段AC绕点A旋转后，使点C落在BA的延长线上的点C′处，
∴AC′=3

2

，
∴C′D=

AD2+AC′2

=

32+(3 2 )2

=

27

=3

3

，
∴cos∠ADC′=

AD

C′D

=

3

3 3

=

3

3

，
故选：A．

点评：本题考查了旋转的性质、勾股定理、正方形的性质、锐角三角函数的定义，注意各知识点之间的联系．