题目内容
如图，△ABC中，∠C=90°，E是AB上一点，且BE=BC，过E作ED⊥AB交AC于D，若AC=7cm，AE=2cm．则△AED的周长为考点：角平分线的性质,勾股定理
专题：
分析：连接BD，根据勾股定理求出DC=DE，求出△AED的周长=AC+AE，代入求出即可．
解答：解：
连接BD，
∵在Rt△DCB和Rt△DEB中，BD=BD，BE=BC，由勾股定理得：DC=DE，
∴△AED的周长为AE+DE+AD=AE+CD+AD=AE+AC=2cm+7cm=9cm，
故答案为：9．
连接BD，
∵在Rt△DCB和Rt△DEB中，BD=BD，BE=BC，由勾股定理得：DC=DE，
∴△AED的周长为AE+DE+AD=AE+CD+AD=AE+AC=2cm+7cm=9cm，
故答案为：9．
点评：本题考查了勾股定理的应用，解此题的关键是求出DE=CD，题目比较典型，难度适中．
练习册系列答案
相关题目
利用图形来表示数量或数量关系，也可以利用数量或数量关系来描述图形特征或图形之间的关系，这种思想方法称为数形结合．如图，一个边长为1的正方形，依次取正方形面积的北京天安门广场前每天早晨都会举行升国旗仪式，在一个晴朗的日子里，从早晨太阳升起的那一刻起到晚上日落前，旗杆在地面上的影子的变化规律是（ ）
| A、先变短，后变长 |
| B、先变长，后变短 |
| C、长度不变，方向改变 |
| D、以上都不正确 |
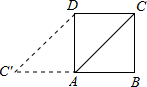如图，正方形ABCD的边长为3，将线段AC绕点A旋转后，使点C落在BA的延长线上的点C′处，则∠ADC′的余弦值为（ ）A、
| ||||
B、
| ||||
C、
| ||||
D、
|