题目内容
15．
如图，圆O的弦AB垂直平分半径OC，若圆O的半径为4，则弦AB的长等于4$\sqrt{3}$．
分析 连接OA，根据弦AB垂直平分半径OC可求出OE的长，再由勾股定理求出AE的长，进而可得出结论．
解答 
解：连接OA，
∵弦AB垂直平分半径OC，OC=4，
∴OE=$\frac{1}{2}$OC=2．
∵OA2=OE2+AE2，即42=22+AE2，解得AE=2$\sqrt{3}$，
∴AB=2AE=4$\sqrt{3}$．
故答案为：4$\sqrt{3}$．
点评 本题考查的是垂径定理，根据题意作出辅助线，构造出直角三角形是解答此题的关键．
练习册系列答案
相关题目
4．在数-$\frac{1}{2}$，-|-3|，+[-（-5）]，（-2）3，中负数的个数是（ ）
| A． | 4个 | B． | 3个 | C． | 2个 | D． | 1个 |
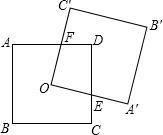如图，正方形ABCD的对角线相交于点O，点O是正方形A′B′C′O的一个顶点．如果两个正方形的边长都等于2，那么正方形A′B′C′OA绕O点无论怎样转动，两个正方形重叠的部分的面积是1．