题目内容
8.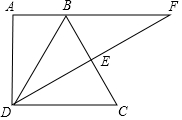 如图,已知在四边形ABCD中,AB∥CD,AD⊥CD,连接BD,BD=DC,E是BC的中点,连接DE并延长,与AB的延长线交于点F.
如图,已知在四边形ABCD中,AB∥CD,AD⊥CD,连接BD,BD=DC,E是BC的中点,连接DE并延长,与AB的延长线交于点F.(1)求证:△DCE≌△FBE;
(2)若∠C=60°,指出图中与DE相等的线段,并说明理由.
分析 (1)由AS证明△DCE≌△FBE即可;
(2)由全等三角形的性质得出FE=DE;证明△BCD是等边三角形,得出∠DBC=∠BDC=60°,证出∠ABD=∠DBC,DE⊥BC,由角平分线的性质即可得出DA=DE∴DA=DE.
解答 (1)证明:∵E是BC的中点,
∴CE=BE,
∵AB∥CD,
∴∠C=∠EBF,
在△DCE和△FBE中,$\left\{\begin{array}{l}{∠C=∠EBF}&{\;}\\{CE=BE}&{\;}\\{∠CED=∠BEF}&{\;}\end{array}\right.$,
∴△DCE≌△FBE(ASA);
(2)解:图中与DE相等的线段是FE、DA;理由如下:
∵△DCE≌△FBE,
∴DE=FE,
∵BD=CD,∠C=60°,
∴△BCD是等边三角形,
∴∠DBC=∠BDC=60°,
∵AB∥CD,AD⊥CD,
∴∠ADC=90°,
∴∠ADB=30°,
∴∠ABD=60°=∠DBC,
∵E是BC的中点,
∴DE⊥BC,
∴DA=DE.
点评 本题考查了全等三角形的判定与性质、平行线的性质、等边三角形的判定与性质、角平分线的性质等知识;熟练掌握全等三角形的判定与性质是解决问题的关键.

练习册系列答案
 全能测控期末小状元系列答案
全能测控期末小状元系列答案
相关题目
 如图,四边形ABCD是⊙O的内接四边形,∠B=148°24′,则∠AOC的角度为63°12′.
如图,四边形ABCD是⊙O的内接四边形,∠B=148°24′,则∠AOC的角度为63°12′.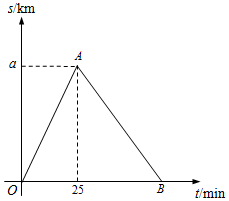 某市举行“迷你马拉松”长跑比赛,运动员从起点甲地出发,跑到乙地后,沿原路线再跑回点甲地.设该运动员离开起点甲地的路程s(km)与跑步时间t(min)之间的函数关系如图所示.已知该运动员从甲地跑到乙地时的平均速度是0.2km/min,根据图象提供的信息,解答下列问题:
某市举行“迷你马拉松”长跑比赛,运动员从起点甲地出发,跑到乙地后,沿原路线再跑回点甲地.设该运动员离开起点甲地的路程s(km)与跑步时间t(min)之间的函数关系如图所示.已知该运动员从甲地跑到乙地时的平均速度是0.2km/min,根据图象提供的信息,解答下列问题: 如图,已知直线l及点A、B,求作⊙O,使得⊙O经过点A、B,且圆心O在直线l上(尺规作图,不写作法,保留作图痕迹).
如图,已知直线l及点A、B,求作⊙O,使得⊙O经过点A、B,且圆心O在直线l上(尺规作图,不写作法,保留作图痕迹).