题目内容
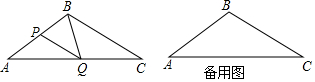
2.如图,在△ABC中,AB=BC=20cm,AC=30cm,点P从A向B运动,速度是4cm/s,点Q从C向A运动,速度是3cm/s,设运动时间为xs,(0<x≤5)(1)当x=$\frac{10}{3}$时,PQ∥BC,
(2)在(1)的条件下S△BCQ:S△ABC=1:3;S△BPQ:S△ABC=2:9;
(3)在P、Q运动的过程中,△APQ与△CQB能否相似,若能求出对应的x值,若不能,请说明理由.
分析 (1)先用含x的式子表示出AP和AQ的长,由$\frac{AP}{AQ}=\frac{AB}{AC}$列方程求解即可;
(2)先求得AP,PB的长,从而得到AP:AB=AQ:QC=2:3,然后依据△BQC和△ABC为等高的三角形,从而可得到S△BCQ:S△ABC=QC:AC,同理可得到S△ABQ=$\frac{2}{3}$S△ACB,S△BPQ=$\frac{1}{3}$S△ABQ,故可求得S△BPQ:S△ABC的值;
(3)本题要分两种情况进行讨论.已知∠A和∠C对应相等,那么就要分成AP和CQ对应成比例以及AP和BC对应成比例两种情况来求x的值.
解答 解:(1)由题意可知AP=4x,QC=3x,则AQ=30-3x.
∵当$\frac{AP}{AQ}=\frac{AB}{AC}$时,PQ∥BC,
∴$\frac{4x}{30-3x}=\frac{20}{30}$,解得:x=$\frac{10}{3}$.
故答案为:$\frac{10}{3}$.
(2)∵x=$\frac{10}{3}$,
∴AP=$\frac{40}{3}$,PB=20-$\frac{40}{3}$=$\frac{20}{3}$.
∴AP:PB=AQ:QC=2:1.
∴QC:AC=1:3.
∴S△BQC=$\frac{1}{3}$S△ACB.
∴S△BCQ:S△ABC=1:3
∵AQ:AC=2:3,
∴S△ABQ=$\frac{2}{3}$S△ACB.
∵AP:AB=2:3,
∴S△BPQ=$\frac{1}{3}$S△ABQ=$\frac{1}{3}$×$\frac{2}{3}$S△ACB=$\frac{2}{9}$S△ACB,
∴S△BPQ:S△ABC=2:9,
故答案为:1:3;2:9.
(3)情况1:当△APQ∽△CQB时,CQ:AP=BC:AQ,即$\frac{3x}{4x}=\frac{20}{30-3x}$,解得x=$\frac{10}{9}$,
经检验,x=$\frac{10}{9}$是原分式方程的解.
情况2:当△APQ∽△CBQ时,CQ:AQ=BC:AP,即$\frac{3x}{30-3x}=\frac{20}{4x}$,解得x=5,
经检验,x=5是原分式方程的解.
综上所述:当x=$\frac{10}{9}$或x=5时,△APQ与△CQB相似.
点评 本题主要考查的是相似三角形的综合应用,解答本题需要同学们熟练掌握相似三角形的性质和判定定理,找出图形中等高的三角形的是解答问题(2)的关键,分类讨论是解答问题(3)的关键.

| A. | y=x2-2 | B. | y=x2+2 | C. | y=(x-2)2 | D. | y=(x+2)2 |

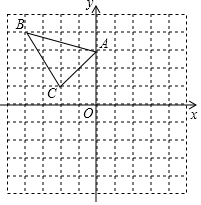 △ABC在直角坐标系内的位置如图.
△ABC在直角坐标系内的位置如图. 如图,点E,F是正方形ABCD的对角线BD所在直线上的两点,且BE=DF,∠EAB=15°.则$\frac{BE}{AB}$=$\frac{\sqrt{6}-\sqrt{2}}{2}$.
如图,点E,F是正方形ABCD的对角线BD所在直线上的两点,且BE=DF,∠EAB=15°.则$\frac{BE}{AB}$=$\frac{\sqrt{6}-\sqrt{2}}{2}$.