题目内容
19. 如图,抛物线y=-x2+$\frac{7}{2}$x+2与y轴交于点A,与x轴的正半轴交于点B,作垂直于x轴的直线x=t,在第一象限交直线AB于M,交抛物线于N,求当t取何值时,MN有最大值?最大值是多少?
如图,抛物线y=-x2+$\frac{7}{2}$x+2与y轴交于点A,与x轴的正半轴交于点B,作垂直于x轴的直线x=t,在第一象限交直线AB于M,交抛物线于N,求当t取何值时,MN有最大值?最大值是多少?
分析 首先令y=-x2+$\frac{7}{2}$x+2=0,求出B点的坐标,设直线AB的解析式为y=kx+b,根据题意求出直线AB的解析式,然后根据点N在抛物线上,点M在直线AB上,求出点N(t,-t2+$\frac{7}{2}$t+2),点M(t,-$\frac{1}{2}$t+2),列出MN关于t的一元二次方程,结合二次函数的性质,求出最值.
解答 解:令y=-x2+$\frac{7}{2}$x+2=0,
则2x2-7x-4=0,
解得x=-$\frac{1}{2}$或x=4,
∴点B坐标为(4,0),
令x=0,则y=2,
则点A的坐标为(0,2),
设直线AB的解析式为y=kx+b,
则$\left\{\begin{array}{l}{4k+b=0}\\{b=2}\end{array}\right.$,
解得$\left\{\begin{array}{l}{k=-\frac{1}{2}}\\{b=2}\end{array}\right.$,
即直线AB的解析式为y=-$\frac{1}{2}$x+2,
又知点N在抛物线上,点M在直线AB上,
则点N(t,-t2+$\frac{7}{2}$t+2),点M(t,-$\frac{1}{2}$t+2),
MN=-t2+$\frac{7}{2}$t+2-(-$\frac{1}{2}$t+2)=-t2+4t=-(t-2)2+4,
当t=2时,MN有最大值为4.
点评 本题主要考查了抛物线与x轴交点的知识,解答本题的关键是求出直线AB的解析式,此题难度不大.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图,在△ABC中,AD是角平分线,AE是高,∠BAC=40°,∠C=60°,求∠DAE的度数.
如图,在△ABC中,AD是角平分线,AE是高,∠BAC=40°,∠C=60°,求∠DAE的度数.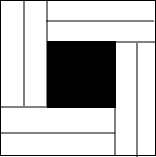 如图所示的正方形是由八块相同的长方形拼制而成的,且长与宽之比为4:1,中间留下一个边长为2mm的小正方形,你能求出长方形的长与宽吗?大正方形的面积是多少?
如图所示的正方形是由八块相同的长方形拼制而成的,且长与宽之比为4:1,中间留下一个边长为2mm的小正方形,你能求出长方形的长与宽吗?大正方形的面积是多少? 如图,正方形ABCD的面积为4cm2,则图中阴影部分的面积为2cm2.
如图,正方形ABCD的面积为4cm2,则图中阴影部分的面积为2cm2.