Question

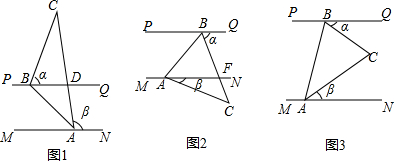
8．已知，直线PQ∥MN，△ABC的顶点A与B分别在直线MN与PQ上，点C在直线AB的右侧，且∠CAB=∠C=45°，设∠CBQ=∠α，∠CAN=∠β．
（1）如图1，当点C落在PQ的上方时，AC与PQ相交与点D，求证：∠β=∠α+45°．
请将下列推理过程补充完整：
证明：∵∠CDQ是△CBD的一个外角（三角形外角的定义），
∴∠CDQ=∠α+∠C（三角形的一个外角等于和它不相邻的两个内角的和）
∵PQ∥MN（已知），
∴∠CDQ=∠β（两直线平行，同位角相等）
∴∠β=∠α+∠C（等量代换）．
∵∠C=45°（已知），
∴∠β=∠α+45°（等量代换）
（2）如图2，当点C落在直线MN的下方时，BC与MN交于点F，求证：∠α=∠β+45°；
（3）如图3，当点C落在直线PQ和MN之间时，直接写出∠α、∠β与45°三者之间的一个等量关系．

Answer 1

分析 （1）根据题意可以写出推理过程，从而可以解答本题；
（2）根据题意和图形可以解答本题；
（3）先写出数量关系，再进行证明即可解答本题．

解答 （1）证明：∵∠CDQ是△CBD的一个外角（三角形外角的定义），
∴∠CDQ=∠α+∠C（三角形的一个外角等于和它不相邻的两个内角的和）
∵PQ∥MN（已知），
∴∠CDQ=∠β（两直线平行，同位角相等）
∴∠β=∠α+∠C（等量代换）．
∵∠C=45°（已知），
∴∠β=∠α+45°（等量代换）
故答案为：已知；两直线平行，同位角相等；∠α+∠C；
（2）证明：∵∠CFN是△ACF的一个外角（三角形外角的定义），
∴∠CFN=∠β+∠C（三角形的一个外角等于和它不相邻的两个内角的和
∵PQ∥MN（已知），
∴∠CFN=∠α（两直线平行，同位角相等）
∴∠α=∠β+∠C（等量代换）．
∵∠C=45°（已知），
∴∠α=∠β+45°（等量代换）；
（3）∠α+∠β=45°，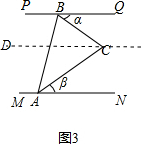
理由：在图3中，作CD∥PQ，
则CD∥MN，
∴∠α=∠BCD，∠DCA=∠β，
∵∠BCA=∠BCD+∠DCA，∠BCA=45°，
∴∠α+∠β=∠BCA，
∴∠α+∠β=45°．

点评 本题考查平行线的性质，解题的关键是明确题意，找出所求问题需要的条件，利用数形结合的思想解答．