题目内容
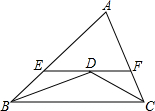 如图,在△ABC中,BD、CD分别平分∠ABC、∠ACB,过点D作直线平行于BC,交AB、AC于点E、F,当∠A的位置及大小变化时,线段EF和BE+CF的大小关系为( )
如图,在△ABC中,BD、CD分别平分∠ABC、∠ACB,过点D作直线平行于BC,交AB、AC于点E、F,当∠A的位置及大小变化时,线段EF和BE+CF的大小关系为( )| A、EF>BE+CF |
| B、EF=BE+CF |
| C、EF<BE+CF |
| D、不能确定 |
考点:等腰三角形的判定与性质,平行线的性质
专题:
分析:由平行线的性质和角平分线的定义可得∠EBD=∠EDB,则ED=BE,同理可得DF=FC,则EF=BE+CF,可得答案.
解答:解:∵EF∥BC,
∴∠EDB=∠DBC,
∵BD平分∠ABC,
∴∠EBD=∠DBC,
∴∠EDB=∠EBD,
∴ED=BE,
同理DF=FC,
∴ED+DF=BE+FC,
即EF=BE+FC,
故选B.
∴∠EDB=∠DBC,
∵BD平分∠ABC,
∴∠EBD=∠DBC,
∴∠EDB=∠EBD,
∴ED=BE,
同理DF=FC,
∴ED+DF=BE+FC,
即EF=BE+FC,
故选B.
点评:本题主要考查等腰三角形的判定,利用平行线的性质及角平分线的定义得到ED=BE和DF=FC是解题的关键

练习册系列答案
 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
 如图,已知AB是直径,弦CD与AB相交于点P,且将AB分成2和8两段,∠DPB=30°,求弦CD的长.
如图,已知AB是直径,弦CD与AB相交于点P,且将AB分成2和8两段,∠DPB=30°,求弦CD的长. 有理数a,b在数轴的位置如图,则下面关系中正确的个数为( )
有理数a,b在数轴的位置如图,则下面关系中正确的个数为( )