题目内容
已知△ABC的内切圆O分别与三边BC、CA、AB相切于点D、E、F,∠DEF=70°,求∠ABC的度数.
考点:三角形的内切圆与内心
专题:计算题
分析:连结OF、OD,如图,先根据圆周角定理得∠FOD=2∠DEF=140°,再根据内切圆的定义和切线的性质得∠BFO=∠BDO=90°,然后根据四边形内角和计算∠ABC的度数.
解答:解: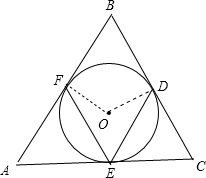 连结OF、OD,如图,
连结OF、OD,如图,
∵∠DEF=70°,
∵∠FOD=2∠DEF=140°,
∵△ABC的内切圆I分别与三边BC、AB相切于点D、F,
∴OF⊥AB,OD⊥BC,
∴∠BFO=∠BDO=90°,
∴∠B+∠FOD=180°,
∴∠B=180°-140°=40°.
 连结OF、OD,如图,
连结OF、OD,如图,∵∠DEF=70°,
∵∠FOD=2∠DEF=140°,
∵△ABC的内切圆I分别与三边BC、AB相切于点D、F,
∴OF⊥AB,OD⊥BC,
∴∠BFO=∠BDO=90°,
∴∠B+∠FOD=180°,
∴∠B=180°-140°=40°.
点评:本题考查了三角形的内切圆与内心:与三角形各边都相切的圆叫三角形的内切圆,三角形的内切圆的圆心叫做三角形的内心,这个三角形叫做圆的外切三角形.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图,将方格纸中的图形绕点O逆时针旋转90°后得到的图形是( )
如图,将方格纸中的图形绕点O逆时针旋转90°后得到的图形是( )A、 |
B、 |
C、 |
D、 |
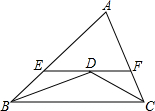 如图,在△ABC中,BD、CD分别平分∠ABC、∠ACB,过点D作直线平行于BC,交AB、AC于点E、F,当∠A的位置及大小变化时,线段EF和BE+CF的大小关系为( )
如图,在△ABC中,BD、CD分别平分∠ABC、∠ACB,过点D作直线平行于BC,交AB、AC于点E、F,当∠A的位置及大小变化时,线段EF和BE+CF的大小关系为( )| A、EF>BE+CF |
| B、EF=BE+CF |
| C、EF<BE+CF |
| D、不能确定 |
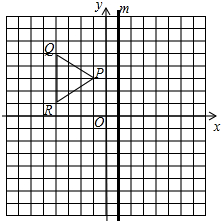 如图,△PQR在平面直角坐标系中所示位置,在直线m上各点的横坐标都为1
如图,△PQR在平面直角坐标系中所示位置,在直线m上各点的横坐标都为1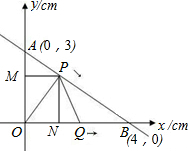 已知,Rt△ABC中,∠AOB=90°,OA=3cm,OB=4cm,以O为坐标原点建立如图所示的直角坐标系,设P、Q分别为AB边、OB边上的动点,它们同时分别从A、O向B匀速移动,速度都为1cm/s,设PQ移动时间为ts(0≤t≤4).
已知,Rt△ABC中,∠AOB=90°,OA=3cm,OB=4cm,以O为坐标原点建立如图所示的直角坐标系,设P、Q分别为AB边、OB边上的动点,它们同时分别从A、O向B匀速移动,速度都为1cm/s,设PQ移动时间为ts(0≤t≤4). 学校要把校园内一块长20米,宽12米的长方形空地进行绿化,计划中间种花,四周留出宽度相同的地种草坪,且花坛面积为180平方米,求草坪的宽度.
学校要把校园内一块长20米,宽12米的长方形空地进行绿化,计划中间种花,四周留出宽度相同的地种草坪,且花坛面积为180平方米,求草坪的宽度. 在直角坐标系内的位置如图所示:
在直角坐标系内的位置如图所示: