题目内容
5.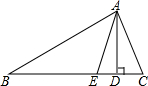 如图,在△ABC中,AD、AE分别是△ABC的高和角平分线,∠B=30°,∠C=50°.
如图,在△ABC中,AD、AE分别是△ABC的高和角平分线,∠B=30°,∠C=50°.(1)求∠DAE的度数;
(2)试写出∠DAE与∠C、∠B之间的数量关系(不必说明理由).
分析 (1)由AD是BC边上的高可得出∠ADE=90°,在△ABC中利用三角形内角和定理可求出∠BAC的度数,由角平分线的定义可求出∠BAE的度数,再根据三角形外角的性质可求出∠AED的度数,在△ADE中利用三角形内角和定理可求出∠DAE的度数;
(2)∠DAE=$\frac{1}{2}$(∠C-∠B),理由同(1).
解答 解:(1)∵AD是BC边上的高,
∴∠ADE=90°.
∵∠BAC+∠B+∠C=180°,
∴∠BAC=180°-∠B-∠C=100°.
∵AE是∠BAC平分线,
∴∠BAE=$\frac{1}{2}$∠BAC=50°,
∴∠AED=∠B+∠BAE=30°+50°=80°.
∵∠ADE+∠AED+∠DAE=180°,
∴∠DAE=180°-∠ADE-∠AED=180°-90°-80°=10°.
(2)∠DAE=$\frac{1}{2}$(∠C-∠B),理由如下:
∵AD是BC边上的高,
∴∠ADE=90°.
∵∠BAC+∠B+∠C=180°,
∴∠BAC=180°-∠B-∠C.
∵AE是∠BAC平分线,
∴∠BAE=$\frac{1}{2}$∠BAC=90°-$\frac{1}{2}$(∠B+∠C),
∴∠AED=∠B+∠BAE=90°+$\frac{1}{2}$(∠B-∠C).
∵∠ADE+∠AED+∠DAE=180°,
∴∠DAE=180°-∠ADE-∠AED=180°-90°-[90°+$\frac{1}{2}$(∠B-∠C)]=$\frac{1}{2}$(∠C-∠B).
点评 本题考查了三角形内角和定理以及三角形外角的性质,解题的关键是:(1)利用三角形外角的性质求出∠AED的度数;(2)重复(1)找出∠DAE=$\frac{1}{2}$(∠C-∠B).

练习册系列答案
相关题目
10.“每天锻炼一小时,健康生活一辈子”,自开展“阳光体育运动”以来,学校师生的锻炼意识都增强了.某校有学生8200人,为了解学生每天的锻炼时间,学校体育组随机调查了部分学生,统计结果如表所示.
表格中,m=30人; 这组数据的众数是14.5分钟;该校每天锻炼时间达到1小时的约有820人人.
表格中,m=30人; 这组数据的众数是14.5分钟;该校每天锻炼时间达到1小时的约有820人人.
| 时间段 | 频数 | 频率 |
| 29分钟及以下 | 108 | 0.54 |
| 30-39分钟 | 24 | 0.12 |
| 40-49分钟 | m | 0.15 |
| 50-59分钟 | 18 | 0.09 |
| 1小时及以上 | 20 | 0.1 |
14. 如图,四边形ABCD是正方形,AE垂直于BE,且AE=6,BE=8,则阴影部分的面积是( )
如图,四边形ABCD是正方形,AE垂直于BE,且AE=6,BE=8,则阴影部分的面积是( )
 如图,四边形ABCD是正方形,AE垂直于BE,且AE=6,BE=8,则阴影部分的面积是( )
如图,四边形ABCD是正方形,AE垂直于BE,且AE=6,BE=8,则阴影部分的面积是( )| A. | 66 | B. | 76 | C. | 64 | D. | 100 |

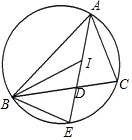 如图,点I是△ABC的内心,AI的延长线与边BC相交于点D,与△ABC的外接圆相交于点C.
如图,点I是△ABC的内心,AI的延长线与边BC相交于点D,与△ABC的外接圆相交于点C.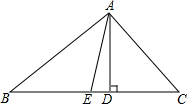 已知:如图,在△ABC中,AD是BC边上的高,AE是∠BAC平分线,∠B=30°,∠DAE=15°,
已知:如图,在△ABC中,AD是BC边上的高,AE是∠BAC平分线,∠B=30°,∠DAE=15°,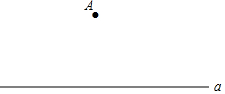 如图,已知直线a和直线a外一点A.
如图,已知直线a和直线a外一点A.