题目内容
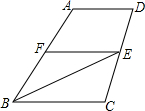 已知:梯形ABCD中,AD∥BC,E是CD中点,且BE平分∠ABC.求证:AB=AD+BC.
已知:梯形ABCD中,AD∥BC,E是CD中点,且BE平分∠ABC.求证:AB=AD+BC.考点:全等三角形的判定与性质,角平分线的性质,梯形中位线定理
专题:证明题
分析:延长BE交AD的延长线于G,由AD∥BC,可得∠G=∠EBC,∠C=∠GDE,由E是CD中点,可得DE=EC,根据AAS可证△DEG≌△CEB,可得DG=BC,进而可得AD+BC=AD+DG=AG,然后由BE平分∠ABC,可得∠ABG=∠EBC,进而得到∠ABG=∠G,然后根据等角对等边,可得AB=AG,进而可得AB=AD+BC.
解答:证明:延长BE交AD的延长线于G,
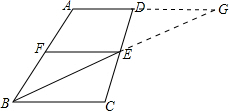
∵AD∥BC,
∴∠G=∠EBC,∠C=∠GDE,
∵E是CD中点,
∴DE=EC,
在△DEG和△CEB中,
,
∴△DEG≌△CEB(AAS),
∴DG=BC,
∴AD+BC=AD+DG=AG,
∵BE平分∠ABC,
∴∠ABG=∠EBC,
∴∠ABG=∠G,
∴AB=AG,
∴AB=AD+BC.

∵AD∥BC,
∴∠G=∠EBC,∠C=∠GDE,
∵E是CD中点,
∴DE=EC,
在△DEG和△CEB中,
|
∴△DEG≌△CEB(AAS),
∴DG=BC,
∴AD+BC=AD+DG=AG,
∵BE平分∠ABC,
∴∠ABG=∠EBC,
∴∠ABG=∠G,
∴AB=AG,
∴AB=AD+BC.
点评:本题考查了角平分线的定义,全等三角形的判定与性质,熟记性质并作辅助线构造出全等三角形是解题的关键.

练习册系列答案
 走进文言文系列答案
走进文言文系列答案
相关题目
依依买了7本数学书和2本语文书共花了100元;菲菲买了4本语文书和2本数学书共花了80元.则买3本数学书要花( )元.
| A、30 | B、20 | C、15 | D、45 |
已知a与b互为相反数,且b≠0,下列各式不成立的是( )
| A、a+b=0 | ||
| B、a2=b2 | ||
| C、|a|=-|b| | ||
D、
|
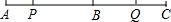 如图所示,线段AC上有一点B,且AB=40cm,BC=30cm,点P从A点出发,沿AC方向以3cm/秒的速度匀速向C点运动,点Q从C点出发,沿CA方向以a cm/秒的速度匀速向A点运动,两点同时出发(P、Q只在线段AC上运动).
如图所示,线段AC上有一点B,且AB=40cm,BC=30cm,点P从A点出发,沿AC方向以3cm/秒的速度匀速向C点运动,点Q从C点出发,沿CA方向以a cm/秒的速度匀速向A点运动,两点同时出发(P、Q只在线段AC上运动).