题目内容
先化简，再求值
（1）（
-1）÷
．其中a=
+1，b=
-1
（2）
-
-
，其中a=-1-
．
（1）（
| a |
| a-b |
| b |
| a2-b2 |
| 3 |
| 3 |
（2）
| a2-1 |
| a-1 |
| ||
| a2+a |
| 1 |
| a |
| 3 |
考点：分式的化简求值,二次根式的化简求值
专题：计算题
分析：（1）原式括号中两项通分并利用同分母分式的减法法则计算，同时利用除法法则变形，约分得到最简结果，把a与b的值代入计算即可求出值；
（2）原式利用二次根式的性质化简，把a的值代入计算即可求出值．
（2）原式利用二次根式的性质化简，把a的值代入计算即可求出值．
解答：解：（1）原式=
•
=a+b，
当a=
+1，b=
-1时，原式=2
；
（2）∵a=-1-
，
∴a+1=-
＜0，
则原式=a+1+
-
=a+1=-
．
| a-a+b |
| a-b |
| (a+b)(a-b) |
| b |
当a=
| 3 |
| 3 |
| 3 |
（2）∵a=-1-
| 3 |
∴a+1=-
| 3 |
则原式=a+1+
| a+1 |
| a(a+1) |
| 1 |
| a |
| 3 |
点评：此题考查了分式的化简求值，熟练掌握运算法则是解本题的关键．
练习册系列答案
期末100分闯关海淀考王系列答案
小学能力测试卷系列答案
相关题目
关于x的一元二次方程x2-（2m-1）x+m+3=0的两根为x1，x2，且满足x1x2-x1-x2=1，则m的值为（ ）
| A、3 | ||
| B、-3 | ||
C、
| ||
D、-
|
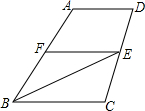已知：梯形ABCD中，AD∥BC，E是CD中点，且BE平分∠ABC．求证：AB=AD+BC．下列分式是最简分式的是（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|