Question

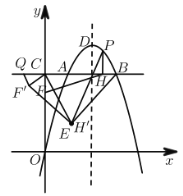
【题目】如图，平面直角坐标系中，点，函数（）的图象经过平行四边形的顶点和边的中点.

（1）求的值；

（2）若的面积等于6.求的值；

（3）若为函数（）的图象上一个动点，过点作直线轴于点，直线与轴上方的平行四边形的一边交于点，设点的横坐标为，当时，求的值.

Answer 1

【答案】（1）；（2）；（3）或.

【解析】

（1）根据平行四边形的性质确定出B的坐标从而确定出D的坐标，而点A，D在反比例函数图象上，建立方程求出m，

（2）根据三角形OAD的面积是平行四边形OABC面积的一半，确定出n即可；

（3）根据题意可得情况讨论①点在上，②当点在上，求出两种情况下点M,N,P的坐标，即可求出MP，NP的长度结合，求解即可.

解：（1）∵点，平行四边形的顶点

∴

∴

∵函数（）的图象经过平行四边形的顶点和边的中点

∴，

∴

（2）∵点是平行四边形中点

∴

∵

∴

由（1）知，

∴

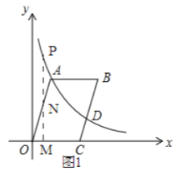
（3）①如图1，点在上，

由（1）知，

∴

即

直线的解析式为，

设点的横坐标为

∴

∵过点作直线轴于点

∴，

∴，

∵

∴

∴或（舍）

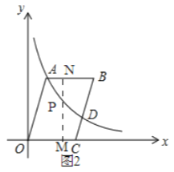
②如图2，

当点在上时，

由（1）知，

∴

由题意知，，，

∵

∴

∴