Question

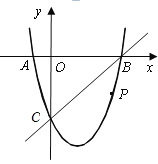
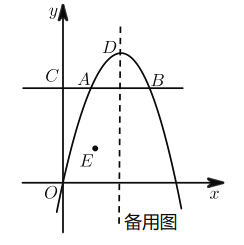
【题目】如图，在平面直角坐标系中，点A在抛物线y=- x2 + 4x上，且横坐标为1，点B与点A关于抛物线的对称轴对称，直线AB与y轴交于点C，点D为抛物线的顶点，点E的坐标为(1，1).

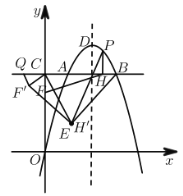
(1)求线段AB的长.

(2)点P为线段AB.上方抛物线上的任意一点，过点P作AB的垂线交AB于点H，点F为y轴上一点，当PBE的面积最大时，求PH + HF + FO的最小值.

(3)在(2)中，PH+HF+方FO取得最小值时，将CFH绕点C顺时针旋转60°后得到CF'H'，过点F'作CF'的垂线与直线AB交于点Q，点R为抛物线对称轴上的一点，在平面直角坐标系中是否存在点S，使以点D，Q，R，S为顶点的四边形为菱形，若存在，请直接写出点S的坐标，若不存在，请说明理由.

Answer 1

【答案】(1) AB=2；(2) ；(3) (-1，3-)或( -1，3 + )或( -1，8)或(5，3).

【解析】

（1）求出A、B两点坐标，即可解决问题；
（2）如图1中，设P（m，-m2+4m），作PN∥y轴交BE于N．构建二次函数利用二次函数的性质求出满足条件的点P坐标，作直线OG交AB于G，使得∠COG=30°，作HK⊥OG于K交OC于F，因为FK=OF，推出PH+HF+FO=PH+FH+Fk=PH+HK，此时PH+HF+OF的值最小，解直角三角形即可解决问题；
（3）分两种情形分别求解即可.

解：（1）由题意A（1，3），B（3，3），
∴AB=2；

（2）如图1中，

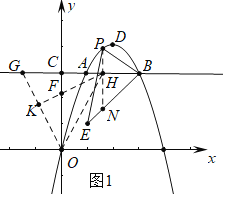
设P（m，-m2+4m），作PN∥y轴交BE于N．
∵直线BE的解析式为y=x，
∴N（m，m），
∴S△PEB=×2×（-m2+3m）=-m2+3m，
∴当m=时，△PEB的面积最大，此时P（，），H（，3），
∴PH=-3=，
作直线OG交AB于G，使得∠COG=30°，作HK⊥OG于K交OC于F，
∵FK=OF，
∴PH+HF+FO=PH+FH+FK=PH+HK，此时PH+HF+OF的值最小，
∵HGOC=OGHK，
∴HK= ，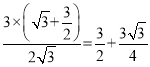
∴PH+HF+OF的最小值为．

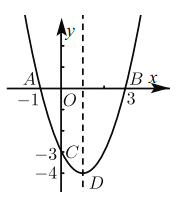
（3）如图2中，由题意CH=，CF=，QF′=，CQ=1，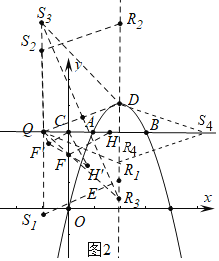

∴Q（-1，3），D（2，4），DQ=，
①当DQ为菱形的边时，S1（-1，3-），S2（-1，3+），S4（5，3）
②当DQ为对角线时，可得S3（-1，8），
综上所述，满足条件的点S坐标为（-1，3-）或（-1，3+）或（-1，8）或（5，3）．