题目内容
7.已知反比例函数$y=\frac{k-2}{x}$在其图象所在的每一个象限内,y的值随着x的值的增大而减小,则k的取值范围是( )| A. | k<2 | B. | k≤2 | C. | k>2 | D. | k≥2 |
分析 先根据反比例函数$y=\frac{k-2}{x}$的图象在每一个象限内,y随x的增大而减小得出关于k的不等式,求出k的取值范围即可.
解答 解:∵反比例函数$y=\frac{k-2}{x}$的图象在每一个象限内,y随x的增大而减小,
∴k-2>0,
∴k>>2.
故选C.
点评 本题考查的是反比例函数的性质,即反比例函数y=$\frac{k}{x}$(k≠0)的图象是双曲线,当k<0,双曲线的两支分别位于第二、第四象限,在每一象限内y随x的增大而增大.

练习册系列答案
 全程金卷系列答案
全程金卷系列答案
相关题目
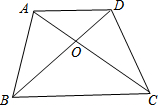 梯形ABCD中,AD∥BC,对角线AC、BD交于点O,若AD=3,BC=5,则S△AOD:S△DOC=3:5.
梯形ABCD中,AD∥BC,对角线AC、BD交于点O,若AD=3,BC=5,则S△AOD:S△DOC=3:5.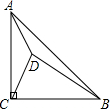 如图,在等腰△ABC中,∠ACB=90°,AC=BC,D为△ABC内一点,且DA=1,DC=2,DB=3.求∠ADC的度数.
如图,在等腰△ABC中,∠ACB=90°,AC=BC,D为△ABC内一点,且DA=1,DC=2,DB=3.求∠ADC的度数. 如图是1973年甘肃出土的陶罐,忽略陶罐的两个抓柄,它可以看做是一个平面图形绕一条直线旋转一周产生的,请画出这个平面图形以及旋转轴的位置.
如图是1973年甘肃出土的陶罐,忽略陶罐的两个抓柄,它可以看做是一个平面图形绕一条直线旋转一周产生的,请画出这个平面图形以及旋转轴的位置.