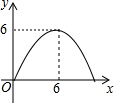题目内容
13.在实数:3.14159,$\sqrt{\frac{9}{16}}$,2+$\sqrt{3}$,$\root{3}{5}$-$\root{3}{64}$,3.212212221…(相邻两个1之间2的个数逐次加1),4.$\stackrel{••}{21}$,π,$\frac{22}{7}$中,无理数有( )| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
分析 无限不循环小数为无理数,由此可得出无理数的个数.
解答 解:在实数:3.14159,$\sqrt{\frac{9}{16}}$,2+$\sqrt{3}$,$\root{3}{5}$-$\root{3}{64}$,3.212212221…(相邻两个1之间2的个数逐次加1),4.$\stackrel{••}{21}$,π,$\frac{22}{7}$中,无理数有2+$\sqrt{3}$,$\root{3}{5}$-$\root{3}{64}$,3.212212221…(相邻两个1之间2的个数逐次加1),π,
故选C
点评 此题主要考查了无理数的定义,其中初中范围内学习的无理数有:π,2π等;开方开不尽的数;以及像0.1010010001…,等有这样规律的数.

练习册系列答案
相关题目
3. 如图,点A表示的实数是( )
如图,点A表示的实数是( )
 如图,点A表示的实数是( )
如图,点A表示的实数是( )| A. | $\sqrt{3}$ | B. | $\sqrt{5}$ | C. | -$\sqrt{3}$ | D. | -$\sqrt{5}$ |
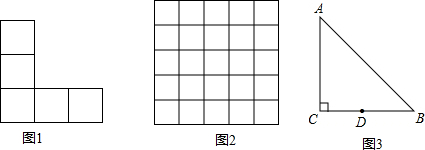
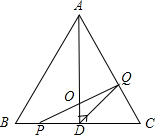 如图,在△ABC中,已知AB=BC=CA=4cm,AD⊥BC于D,点P、Q分别从B、C两点同时出发,其中点P沿BC向终点C运动,速度为1cm/s,点Q沿CA、AB向终点B运动,速度为2cm/s,设它们的运动时间为x(s).
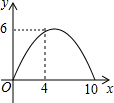
如图,在△ABC中,已知AB=BC=CA=4cm,AD⊥BC于D,点P、Q分别从B、C两点同时出发,其中点P沿BC向终点C运动,速度为1cm/s,点Q沿CA、AB向终点B运动,速度为2cm/s,设它们的运动时间为x(s).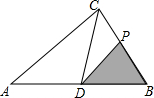 Rt△ABC中,∠ACB=90°,点CD是斜边AB上的中点,BC=4cm,AC=6cm,一动点P从点B出发沿B→C→A路线以1cm/s的速度移动,设△PBD的面积为y(cm2),则y关于点P的运动时间x(s)的函数图象可大致是( )
Rt△ABC中,∠ACB=90°,点CD是斜边AB上的中点,BC=4cm,AC=6cm,一动点P从点B出发沿B→C→A路线以1cm/s的速度移动,设△PBD的面积为y(cm2),则y关于点P的运动时间x(s)的函数图象可大致是( )