题目内容
2.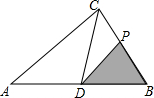 Rt△ABC中,∠ACB=90°,点CD是斜边AB上的中点,BC=4cm,AC=6cm,一动点P从点B出发沿B→C→A路线以1cm/s的速度移动,设△PBD的面积为y(cm2),则y关于点P的运动时间x(s)的函数图象可大致是( )
Rt△ABC中,∠ACB=90°,点CD是斜边AB上的中点,BC=4cm,AC=6cm,一动点P从点B出发沿B→C→A路线以1cm/s的速度移动,设△PBD的面积为y(cm2),则y关于点P的运动时间x(s)的函数图象可大致是( )| A. |  | B. | 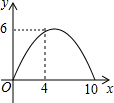 | C. |  | D. | 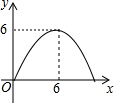 |
分析 作CE⊥AB,PF⊥AB,由BC=4cm,AC=6cm,求出AB、CE的长,由△BPF∽△BCE,用x表示出PF的长,则运用三角形面积公式得到y与x的函数关系式,即可作出选择.
解答 解:当0<x≤4时,如图,作CE⊥AB,PF⊥AB,
∵BC=4cm,AC=6cm,
∴AB=2$\sqrt{13}$,
∴AD=BD=$\sqrt{13}$,
∵AC•BC=AB•CE
∴CE=$\frac{AC•BC}{AB}$=$\frac{24}{2\sqrt{13}}$=$\frac{12\sqrt{13}}{13}$,
∵PF∥CE,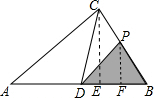
∴△BPF∽△BCE,
∴$\frac{BP}{BC}=\frac{PF}{CE}$,
∴$\frac{x}{4}=\frac{PF}{\frac{12\sqrt{13}}{13}}$,
∴PF=$\frac{3\sqrt{13}}{13}$x,
∴y=$\frac{1}{2}$•BD•PF=$\frac{1}{2}×\sqrt{13}×\frac{3\sqrt{13}}{13}x$=$\frac{3}{2}$x(0<x≤4)
当4<x≤10时,则△APF∽△ACE,
∴$\frac{AP}{AC}=\frac{PF}{CE}$,
∴$\frac{10-x}{6}=\frac{PF}{\frac{12\sqrt{13}}{13}}$,
∴PF=$\frac{2\sqrt{13}}{13}$(10-x),
∴y=$\frac{1}{2}$×$\sqrt{13}$×$\frac{2\sqrt{13}}{13}$(10-x)=10-x(4<x≤10),
故此函数的图象是A选项.
故选A.
点评 本题主要考查了动点函数的图象,根据题意列出函数表达式是做出正确判断的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
10.下列三个命题:①圆既是轴对称图形又是中心对称图形;②垂直于弦的直径平分弦;③相等的圆心角所对的弧相等.其中真命题的是( )
| A. | ①② | B. | ②③ | C. | ①③ | D. | ①②③ |
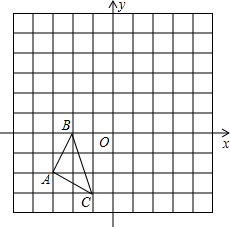 如图,图中每个小正方形的边长都是1个单位长度,O为坐标原点.
如图,图中每个小正方形的边长都是1个单位长度,O为坐标原点.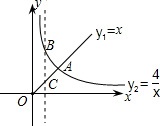 函数y1=x(x≥0),y2=$\frac{4}{x}$(x>0)的图象如图所示,下列结论:
函数y1=x(x≥0),y2=$\frac{4}{x}$(x>0)的图象如图所示,下列结论: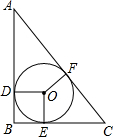 如图,Rt△ABC的内切圆⊙O与AB、BC、AC分别切于点D、E、F,且AC=13,AB=12,∠ABC=90°求:⊙O的半径长.
如图,Rt△ABC的内切圆⊙O与AB、BC、AC分别切于点D、E、F,且AC=13,AB=12,∠ABC=90°求:⊙O的半径长.