题目内容
1.若$\frac{1}{a-b}$+$\frac{1}{a+b}$+$\frac{2a}{{a}^{2}+{b}^{2}}$+$\frac{4{a}^{3}}{{a}^{4}+{b}^{4}}$=15,求a-$\frac{{b}^{8}}{{a}^{7}}$的值.分析 根据通分法则和平方差公式进行计算,然后根据倒数的性质计算即可.
解答 解:∵$\frac{1}{a-b}$+$\frac{1}{a+b}$+$\frac{2a}{{a}^{2}+{b}^{2}}$+$\frac{4{a}^{3}}{{a}^{4}+{b}^{4}}$=15,
∴$\frac{2a}{{a}^{2}-{b}^{2}}$+$\frac{2a}{{a}^{2}+{b}^{2}}$+$\frac{4{a}^{3}}{{a}^{4}+{b}^{4}}$=15,
∴$\frac{4{a}^{3}}{{a}^{4}-{b}^{4}}$+$\frac{4{a}^{3}}{{a}^{4}+{b}^{4}}$=15,
∴$\frac{8{a}^{7}}{{a}^{8}-{b}^{8}}$=15,
∴$\frac{{a}^{7}}{{a}^{8}-{b}^{8}}$=$\frac{15}{8}$,
∴a-$\frac{{b}^{8}}{{a}^{7}}$=$\frac{8}{15}$.
点评 本题考查的是分式的加减运算,掌握通分的法则和平方差公式是解题的关键.

练习册系列答案
 科学实验活动册系列答案
科学实验活动册系列答案
相关题目
11.下面是一位美术爱好者利用网格图设计的几个英文字母的图形,你认为其中是轴对称图形的有( )

| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
11.下列函数中,y是x的反比例函数的是( )
| A. | y=$\frac{x}{7}$ | B. | y=$\frac{1}{2x}$ | C. | y=$\frac{1}{7-x}$ | D. | y=2x |
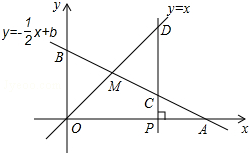 如图,函数y=-$\frac{1}{2}$x+b的图象与x轴、y轴分别交于A、B,与函数y=x的图象交于点M,点M的横坐标为2,在x轴上有一点P(a,0)(其中a>2),硅点P作x轴的垂线,分别交函数y=-$\frac{1}{2}$x+b和y=x的图象于点C、D
如图,函数y=-$\frac{1}{2}$x+b的图象与x轴、y轴分别交于A、B,与函数y=x的图象交于点M,点M的横坐标为2,在x轴上有一点P(a,0)(其中a>2),硅点P作x轴的垂线,分别交函数y=-$\frac{1}{2}$x+b和y=x的图象于点C、D