题目内容
16．已知直线y=kx过点（-$\frac{1}{2}$，3），A是直线y=kx上一点，若过点A向x轴引垂线，垂足为B，且S△ABO=5，求点B的坐标．分析 根据待定系数法，可得函数解析式，根据三角形的面积公式、函数解析式，可得二元一次方程组，解方程组，可得点A的坐标．
解答 解：∵线y=kx过点（-$\frac{1}{2}$，3），
∴-$\frac{1}{2}$k=3，
解得k=-6，
∴函数的解析式y=-6x；
设A点坐标是（x，-6x），
∴S△ABO=$\frac{1}{2}$|x|•|-6x|=5，
解得$\left\{\begin{array}{l}{x=\frac{\sqrt{15}}{3}}\\{y=-2\sqrt{15}}\end{array}\right.$或$\left\{\begin{array}{l}{x=-\frac{\sqrt{15}}{3}}\\{y=2\sqrt{15}}\end{array}\right.$，
则A点坐标是（$\frac{\sqrt{15}}{3}$，-2$\sqrt{15}$）或（-$\frac{\sqrt{15}}{3}$，2$\sqrt{15}$）．
点评 本题考查了待定系数法求正比例函数解析式，熟练掌握待定系数法是解题的关键．
练习册系列答案
相关题目
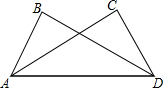如图，在△ADB和△ADC中，有以下条件：①BD=AC，AB=DC；②∠B=∠C，∠BAD=∠CDA；③∠B=∠C，BD=AC；④∠ADB=∠CAD，BD=AC．其中能得出△ADB≌△ADC的是（ ）