题目内容
17．
已知?ABCD，连结对角线BD，E、F是边BC的三等分点，连结AE、AF，与BD分别交于点G、H，则BG：GH：HD的值为5：3：12．
分析 由四边形ABCD是平行四边形，可证得△ADG∽△EBG，△ADH∽△BFH，然后由相似三角形的对应边成比例，求得BG：DG=1：3，BH：DH=2：3，继而求得答案．
解答 解：∵四边形ABCD是平行四边形，
∴AD∥BC，AD=BC，
∴△ADG∽△EBG，△ADH∽△BFH，
∴BG：DG=BE：AD，BH：DH=BF：AD，
∵E、F是边BC的三等分点，
∴BG：DG=1：3，BH：DH=2：3，
∴BG=$\frac{1}{4}$BD，BH=$\frac{2}{5}$BD，DH=$\frac{3}{5}$BD，
∴GH=$\frac{3}{20}$BD，
∴BG：GH：HD=5：3：12．
故答案为：5：3：12．
点评 此题考查了相似三角形的判定与性质以及平行四边形的性质．注意证得△ADG∽△EBG，△ADH∽△BFH是关键．
练习册系列答案
智趣暑假温故知新系列答案
相关题目
7．观察下列各图中小圆点的摆放规律，按这样的规律继续摆放下去，则第⑦个图形中小圆点的个数为（ ）
| A． | 62 | B． | 64 | C． | 66 | D． | 68 |
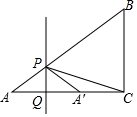如图，Rt△ABC中，∠ACB=90°，AC=4，BC=3，点P为线段AB上一动点，直线PQ⊥AC于点Q，点A关于PQ的对称点A′落在直线AC上，若△A′PC为等腰三角形，则AP的长为$\frac{20}{13}$．
5．下列代数式中，既不是单项式，也不是多项式的是（ ）
| A． | 3x2-2x2+1 | B． | $\frac{5}{2}$xy4 | C． | $\frac{3bc}{a}$ | D． | $\frac{a}{2}$-b |
二次函数y=ax2（a≠0）的图象如图所示，则不等式ax+a＞0的解集是x＞-1．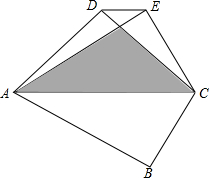
如图，由一副三角板组成的四边形ABCD中，∠B=∠ADC=90°，∠BAC=30°，把△ABC沿AC折叠，点B落在点E处，若两个三角形重叠部分的面积为2$\sqrt{3}$+2，则DE=$\sqrt{2}$．